Question

【题目】如图，直线y= x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（ ）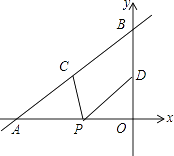

A.（﹣3，0）
B.（﹣6，0）
C.（﹣ ，0）
D.（﹣ ，0）

Answer 1

【答案】C
【解析】解：（方法一）作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．

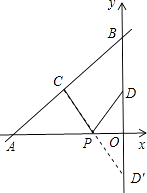
令y= x+4中x=0，则y=4，

∴点B的坐标为（0，4）；

令y= x+4中y=0，则 x+4=0，解得：x=﹣6，

∴点A的坐标为（﹣6，0）．

∵点C、D分别为线段AB、OB的中点，

∴点C（﹣3，2），点D（0，2）．

∵点D′和点D关于x轴对称，

∴点D′的坐标为（0，﹣2）．

设直线CD′的解析式为y=kx+b，

∵直线CD′过点C（﹣3，2），D′（0，﹣2），

∴有 ，解得： ，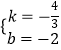

∴直线CD′的解析式为y=﹣ x﹣2．

令y=﹣ x﹣2中y=0，则0=﹣ x﹣2，解得：x=﹣ ，

∴点P的坐标为（﹣ ，0）．

故选C．

（方法二）连接CD，作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图所示．

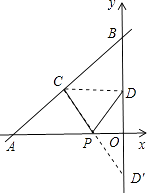
令y= x+4中x=0，则y=4，

∴点B的坐标为（0，4）；

令y= x+4中y=0，则 x+4=0，解得：x=﹣6，

∴点A的坐标为（﹣6，0）．

∵点C、D分别为线段AB、OB的中点，

∴点C（﹣3，2），点D（0，2），CD∥x轴，

∵点D′和点D关于x轴对称，

∴点D′的坐标为（0，﹣2），点O为线段DD′的中点．

又∵OP∥CD，

∴点P为线段CD′的中点，

∴点P的坐标为（﹣ ，0）．

故选C．

（方法一）根据一次函数解析式求出点A、B的坐标，再由中点坐标公式求出点C、D的坐标，根据对称的性质找出点D′的坐标，结合点C、D′的坐标求出直线CD′的解析式，令y=0即可求出x的值，从而得出点P的坐标．

（方法二）根据一次函数解析式求出点A、B的坐标，再由中点坐标公式求出点C、D的坐标，根据对称的性质找出点D′的坐标，根据三角形中位线定理即可得出点P为线段CD′的中点，由此即可得出点P的坐标．