
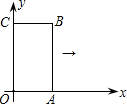
 (2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为
(2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
| k |
| x |
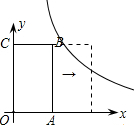 解:设反比例函数解析式为y=
解:设反比例函数解析式为y=| k |
| x |
| k |
| 2 |
| 14 |
| 5 |
| 14 |
| 5x |
| 14 |
| 5n |
| 14 |
| 5(n+1) |
| 14 |
| 5n(n+1) |
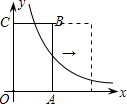 ②与OC,AB平移后的对应边相交;
②与OC,AB平移后的对应边相交;| k |
| 2 |
| 6 |
| 5 |
| 6 |
| 5x |
| 6 |
| 5n |
| 6 |
| 5(n+1) |
| 6 |
| 5n(n+1) |
| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
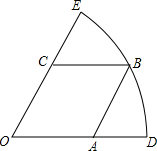 (2012•绍兴)如图,扇形DOE的半径为3,边长为
(2012•绍兴)如图,扇形DOE的半径为3,边长为| 3 |
 |
| DE |
查看答案和解析>>
科目:初中数学 来源: 题型:
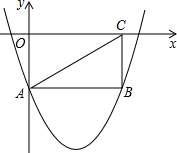 (2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com