练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    为了绿化校园，我校决定修建一块长方形草坪，长米，宽米，并在草坪上修建如图所示的十字路，设小路的宽为米．

    用含的式子分别表示出草坪的面积、小路的面积；

    写出中多项式的项、次数，并说明是几次几项式？

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省无锡市新吴区2018届中考数学模拟试卷 题型：填空题

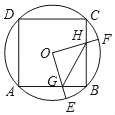
    如图，边长为4的正方形ABCD内接于⊙O，点E是弧AB上的一动点（不与点A、B重合），点F是弧BC上的一点，连接OE，OF，分别与交AB，BC于点G，H，且∠EOF=90°，连接GH，有下列结论：

    ①弧AE=弧BF；②△OGH是等腰直角三角形；③四边形OGBH的面积随着点E位置的变化而变化；④△GBH周长的最小值为4+2．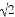

    其中正确的是_____．（把你认为正确结论的序号都填上）

    查看答案和解析>>

    科目：初中数学 来源：苏州市高新区2017-2018学年初三数学第一学期期中考试试卷 题型：解答题

    如图①，直线与抛物线交于不同的两点、 (点在点的左侧).

    （1）直接写出的坐标 ； (用的代数式表示)

    （2）设抛物线的顶点为，对称轴与直线的交点为，连结、，若S△NDC=3×S△MDC，求抛物线的解析式;

    （3）如图②，在(2)的条件下，设该抛物线与轴交于、两点，点为直线下方抛物线上一动点，连接、，设直线交线段于点，△MPQ的面积为，△MAQ的面积为，求的最大值.

    查看答案和解析>>

    科目：初中数学 来源：苏州市高新区2017-2018学年初三数学第一学期期中考试试卷 题型：填空题

    一元二次方程的解为________________________．

    查看答案和解析>>

    科目：初中数学 来源：苏州市高新区2017-2018学年初三数学第一学期期中考试试卷 题型：单选题

    下列四个函数中，图象的顶点在y轴上的函数是( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学上册_第三章_整式及其加减_单元评估测试卷_ 题型：填空题

    有理数，，在数轴上的位置如图所示，则________．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学上册_第三章_整式及其加减_单元评估测试卷_ 题型：填空题

    长方形的长为，宽比长少，则这个长方形的周长是________．

    查看答案和解析>>

    科目：初中数学 来源：安徽省芜湖市部分学校2019届九年级上学期期中联考数学试卷 题型：解答题

    如图所示，在Rt△ABC中，∠ACB＝90°，∠B＝30°，将△ABC绕点C按顺时针方向旋转，可以得到△DEC.若点D刚好落在AB边上，取DE边的中点F，连接FC，试判断四边形ACFD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：第一学期北师大版2019届九年级数学上册期中综合检测试卷（1-4章） 题型：单选题

    的三边之比为，与其相似的的最短边是，则其最长边的长是（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案