
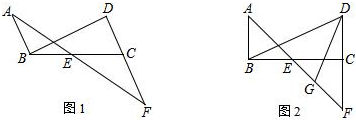
分析 (1)证∠CEF=∠CFE即可,由BE=AB,加上AB∥/CD,结论是显然的;
(2)连接BG,CG,可证△BCG≌△DFG,从而得出△BGD是等腰直角三角形;
解答 解:(1)∵AB=BE,
∴∠BAE=∠BEA,
∵AB∥CD,
∴∠EAB=∠CFE,
∴∠CFE=∠AEB,
∵∠AEB=∠CEF,
∴∠CEF=∠CFE,
∴CE=CF;
(2)如图2,连接AD,CG、BG,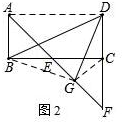
∵AB∥CD,AB=CD,∠ABC=90°,
∴ABCD是矩形,
∵AB=BE,
∴∠BAE=45°,
∴∠FAD=45°,
∴△AFD、△ECF都是等腰直角三角形,
∴DF=AD=BC,
∵G是EF中点,
∴CG=FG,∠BCG=∠DFG=45°,
在△BCG和△DFG中,$\left\{\begin{array}{l}{CG=FG}\\{∠BCG=∠DFG}\\{BC=DF}\end{array}\right.$,
∴△BCG≌△DFG(SAS),
∴∠GBC=∠FDG,BG=DG
∵∠DCB=90°,
∴∠BGD=90°,
∴△BGD是等腰直角三角形,
∴∠BDG=45°.
点评 本题考查了平行四边形的判定与性质、矩形的判定与性质、等腰直角三角形的判定与性质,全等三角形的判定与性质等知识点,难度中等.第(1)问证明两条线段相等,而两条线段在同一个三角形当中,则转化为证角相等,这是常用的处理手段和证明技巧;第(2)问的关键在于巧妙地构造全等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
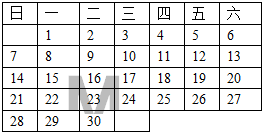 如图是2015年6月份的日历,大写字母M在这张日历上覆盖如图所示的任意7个数,则这7个数的和不可能的是( )
如图是2015年6月份的日历,大写字母M在这张日历上覆盖如图所示的任意7个数,则这7个数的和不可能的是( )| A. | 63 | B. | 75 | C. | 112 | D. | 98 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
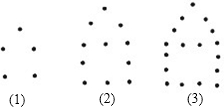 如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.
如图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,摆第四个要23枚棋子,摆第30个“小屋子”要179枚棋子.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2<x1<0 | B. | x1<x2<0 | C. | x2>x1>0 | D. | x1>x2>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com