
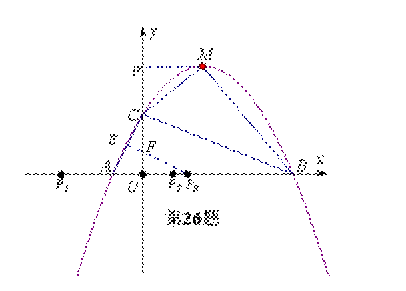
如图,已知抛物线y=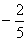 x2+
x2+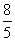 x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C。
x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C。
(1)求点A、B、C的坐标。
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积。
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由。

解:(1)令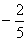 x2+
x2+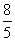 x+2=0,解得
x+2=0,解得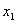 =-1,
=-1,
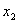 =5……………1分
=5……………1分
令x=0,则y=2,所以A、B、C的坐标分别是A(-1,0)、B(5,0)、C(0,2)……………2分
(2)顶点M的坐标是M(2, )……………3分
)……………3分
过M作MN垂直y轴于N,所以△BCM的面积=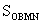 -
-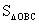 -
- =
=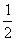 (2+5)×
(2+5)× -
-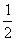 ×5×2-
×5×2-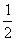 ×(
×( -2)×2=6……………5分
-2)×2=6……………5分
(3)当以AC为腰时,在x轴上有两个点分别为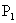 ,
,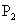 ,易求AC=
,易求AC=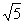 ……………6分
……………6分
则0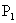 =1+
=1+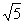 ,O
,O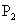 =
=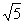 -1,所以
-1,所以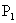 ,
,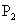 的坐标分别是
的坐标分别是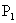 (-1-
(-1-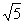 ,0),
,0),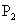 (
(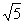 -1,0)
-1,0)
……………7分
当以AC为底时,作AC的垂直平分线交x轴于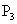 ,交y轴于F,垂足为E,CE=
,交y轴于F,垂足为E,CE=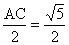
……8分
易证△CEF∽△COA所以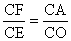 ,而,所以
,而,所以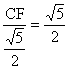 ,CF=
,CF=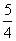
OF=OC-CF=2-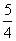 =
=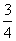 , EF=
, EF=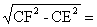
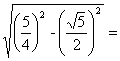
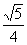 ……………9分
……………9分
又△CEF∽△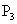 OF,所以,
OF,所以,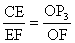 求得O
求得O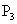 =
=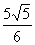
则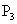 的坐标为
的坐标为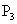 (
(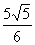 ,0)
,0)
所以存在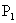 、
、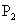 、
、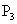 三点,它们的坐标分别是
三点,它们的坐标分别是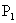 (-1-
(-1-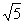 ,0)、
,0)、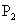 (
(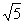 -1,0)、
-1,0)、
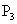 (
(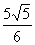 ,0)
,0)


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
如图,在四边形ABCD中,∠1,∠2分别是∠BCD和∠BAD的邻补角,且∠B+∠ADC=140°,则∠1+∠2等于( ).
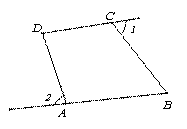
A.140° B.40°
C.260° D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
近年来,我市推行了高效课堂教学模式,以“高效率、高效益、高效果”的特点成为了现代教学的新方向. 为了搞好高效课堂教学,班级学生要进行分组,某校九年级一班共有“优生”和“待优生”45名,且“优生”是“待优生”人数的 ,按相同比例分配到各组,共分成5个组.
,按相同比例分配到各组,共分成5个组.
(1)每个组分配的“优生”和“待优生”各多少名?
(2)高效课堂的第一个环节是预习,一般为10分钟,“优生”最多只需要5分钟,剩下的时间可以指导本组的“待优生”进行预习,从而使本组的预习在规定时间内完成. 如果没有“优生”的指导,“待优生”预习时间最多不能超过多少分钟,才能使本组的总预习时间不超过规定的总预习时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com