
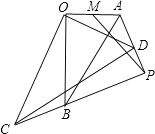
【题目】如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=6,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是( )
A.6﹣3![]() B.6
B.6![]() -6C.3D.
-6C.3D.![]()
【答案】A
【解析】
根据相似三角形的判定定理证明△COB∽△DOA,得到∠OBC=∠OAD,得到∠APB=∠AOB=90°,求出MS和PS,根据三角形三边关系解答即可.
解:取AB的中点S,连接MS、PS,
则PSMS≤PM≤MS+PS,∵∠AOB=90°,OA=6,∠ABO=30°,
∴AB=2OA=12,OB=![]()
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴![]() ,
,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∵∠OBC+∠PBO=180°,
∴∠OAD+∠PBO=180°,∠AOB+∠APB=180°,
∴∠APB=∠AOB=90°,又S是AB的中点,
∴PS=![]() AB=6,
AB=6,
∵M为OA的中点,S是AB的中点,
∴MS=![]() OB=3
OB=3![]() ,
,
∴MP的最小值为63![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校![]() 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
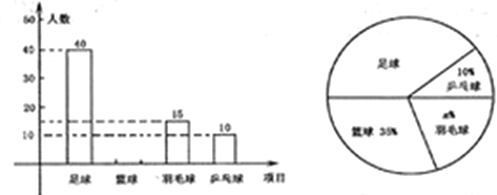
(1)![]() _____________,
_____________,![]() _______________;
_______________;
(2)请补全上图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;
(4)在抽查的![]() 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
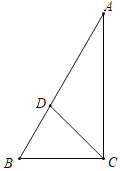
【题目】已知Rt△ABC中,∠ACB=90°,∠B=60°,BC=4,D为AB边上一点,且BD=3,将△BCD绕着点C顺时针旋转60°到△B′CD′,则AD′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
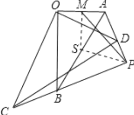
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
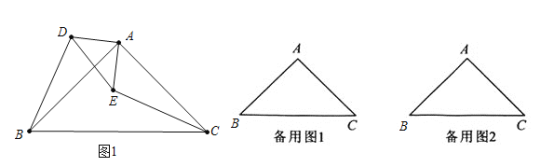
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
,把![]() 绕点A旋转.
绕点A旋转.
![]() 当
当![]() 时,求PB的长;
时,求PB的长;
![]() 直接写出旋转过程中线段PB长的最大值与最小值.
直接写出旋转过程中线段PB长的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况,请你根据图中的信息回答下列问题:
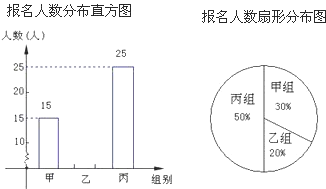
(1)该年级报名参加丙组的人数为 ;
(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,有AB为斜边的等腰直角三角形ABC,其中点A(0,2),点C(﹣1,0),抛物线y=ax2+ax﹣2经过B点.
(1)求B点的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否存在点N(点B除外),使得△ACN仍然是以AC为直角边的等腰直角三角形?若存在,求点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com