
| 测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
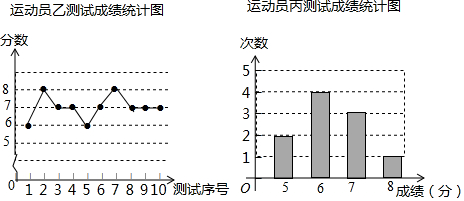
分析 (1)观察表格可知甲运动员测试成绩的众数和中位数都是7分;
(2)易知$\overline{{x}_{甲}}$=7,$\overline{{x}_{乙}}$=7,$\overline{{x}_{丙}}$=6.3,根据方差的意义不难判断.
解答 解:(1)甲运动员测试成绩中7出现最多,故甲的众数为7;
甲成绩重新排列为:5、6、7、7、7、7、7、8、8、8,
∴甲的中位数为$\frac{7+7}{2}$=7,
∴甲测试成绩的众数和中位数都是7分;
(2)$\overline{{x}_{甲}}$=$\frac{1}{10}$×(7+6+8+7+7+5+8+7+8+7)=7,
$\overline{{x}_{乙}}$=$\frac{1}{10}$×(6+6+7+7+7+7+7+7+8+8)=7,
$\overline{{x}_{丙}}$=$\frac{1}{10}$×(5×2+6×4+7×3+8×1)=6.3,
∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,S甲2>S乙2,
∴选乙运动员更合适.
点评 本题考查列表法、条形图、折线图、中位数、平均数、方差等知识,熟练掌握基本概念是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
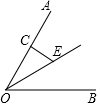 如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.
如图,∠AOB=60°,点E在∠AOB的平分线上,EC⊥OA,且CE=1,点D是OB上的一个动点,当ED取最小值时,线段CD的长度为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2x-10}{3}$-20=$\frac{x-7}{5}$ | B. | $\frac{2x-10}{3}$-2=$\frac{x-7}{5}$ | C. | $\frac{2x-1}{3}$-2=$\frac{x-7}{5}$ | D. | $\frac{2x-1}{3}$-20=$\frac{x-7}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com