
 如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.
如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒. 分析 设AC、AD为正好受影响时,则AC=AD=100,在Rt△ABC中,BC2=AC2-AB2=3600,由此可以求出BC,BD,又拖拉机速度为18米∕秒,让路程除以速度可以计算出受影响时间.
解答 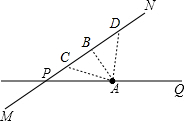 解:作AB⊥DP于B,
解:作AB⊥DP于B,
则AB为A到道路的最短距离.
在Rt△APB中,
∵∠NPQ=30°,
∴sin30°=$\frac{AB}{AP}$,
∴AB=APsin30°=80(米),
在Rt△ABD中,BD=$\sqrt{10{0}^{2}-8{0}^{2}}$=60(米),
∴受影响的时间为:(60×2)÷18=$\frac{20}{3}$(秒),
故答案为:$\frac{20}{3}$.
点评 此题主要考查了勾股定理的应用,解此题的关键是把实际问题转化为数学问题,把实际问题抽象到解直角三角形中,进行解答;注意运用等腰三角形三线合一的性质得到受影响的路程.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
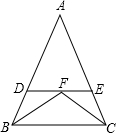 阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,
阅读理解:“在一个三角形中,如果角相等,那么它们所对的边也相等.”简称“等角对等边”,如图,在△ABC中,已知∠ABC和∠ACB的平分线上交于点F,过点F作BC的平行线分别交AB、AC于点D、E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
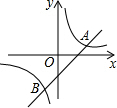 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(-k+4,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com