
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与一次函数y=﹣x+4分别交y轴、x轴于A、B两点.
x2+bx+c与一次函数y=﹣x+4分别交y轴、x轴于A、B两点.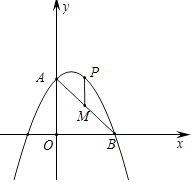
(1)求这个抛物线的解析式;
(2)设P(x,y)是抛物线在第一象限内的一个动点,过点P作直线PH⊥x轴于点H,交直线AB于点M.
①求当x取何值时,PM有最大值?最大值是多少?
②当PM取最大值时,以A、P、M、N为顶点构造平行四边形,求第四个顶点N的坐标.
【答案】
(1)
解:∵一次函数y=﹣x+4分别交y轴、x轴于A、B两点,
∴A(0,4),B(4,0),
把A(0,4),B(4,0)代入y=﹣ ![]() x2+bx+c可得
x2+bx+c可得 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+x+4
x2+x+4
(2)
解:①如图1中,设P(x,﹣ ![]() x2+x+4),则M(x,﹣x+4).
x2+x+4),则M(x,﹣x+4).

∴PM=﹣ ![]() x2+m+4﹣(﹣x+4)=﹣
x2+m+4﹣(﹣x+4)=﹣ ![]() x2+2x=﹣
x2+2x=﹣ ![]() (x﹣2)2+2,
(x﹣2)2+2,
∵﹣ ![]() <0,
<0,
∴x=2时,pM的值最大,最大值为2.
②由①可知P(2,4),M(2,2),

当以A、P、M、N为顶点的四边形为平行四边形时,N1(0,6),N2(4,2),N3(0,2).
【解析】(1)由直线解析式可求得A、B的坐标,再利用待定系数法可求得抛物线的解析式;(2)①可利用x表示出点M的坐标,构建二次函数即可解决问题.②画出图形,满足条件的点N有三个.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(4,0)、(4,n),若经过点O、A的抛物线y=﹣x2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和为 . 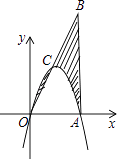
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H. 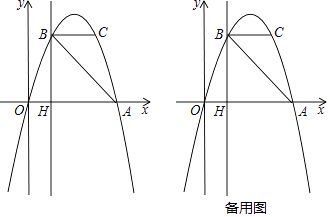
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD,FE分别交AC,BC于点D,E两点,当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),给出以下个结论:①CD=BE ②四边形CDFE不可能是正方形 ③△DFE是等腰直角三角形 ④S四边形CDFE= ![]() S△ABC , 上述结论中始终正确的有( )
S△ABC , 上述结论中始终正确的有( ) 
A.①②③
B.②③④
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为 ![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣2(m+1)x+m2+5=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若原方程的两个实数根为x1、x2 , 且满足x12+x22=|x1|+|x2|+2x1x2 , 求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=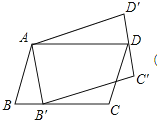
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com