
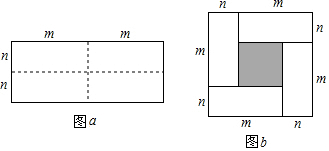
分析 (1)观察得到长为m,宽为n的长方形的长宽之差即为阴影部分的正方形的边长;
(2)根据长方形面积公式可求图a中四个长方形的面积和;可以用大正方形的面积减去先方形的面积得到图b中四个小长方形的面积和;
(3)利用(2)可以得到(m+n)2-(m-n)2=4mn;
(4)根据(3)的结论得到(2x-2y)2=4(x-y)2=4(x+y)2-16xy,然后把x+y=8,xy=7代入计算.
解答 解:(1)图b中的阴影部分的正方形的边长等于长为m,宽为n的长方形的长宽之差,即m-n;
(2)图a中四个长方形的面积和为4mn;图b中四个小长方形的面积和还可以表示为(m+n)2-(m-n)2;
(3)(m+n)2-(m-n)2=4mn;
(4)(2x-2y)2=4(x-y)2=4(x+y)2-16xy,
当x+y=8,xy=7时,原式=256-112=144.
故答案为:m-n;4mn;(m+n)2-4mn;(m+n)2-(m-n)2=4mn;144.
点评 本题考查了完全平方公式的几何背景:利用几何图形之间的面积关系得到完全平方公式.


科目:初中数学 来源: 题型:解答题
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
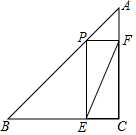 如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=4,点P是AB上的一个动点(点P与点A、B不重合),过点P分别作PE⊥BC于点E,PF⊥AC于点F,连接EF.
如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=4,点P是AB上的一个动点(点P与点A、B不重合),过点P分别作PE⊥BC于点E,PF⊥AC于点F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
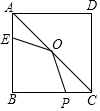 如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )
如图,在正方形ABCD中,边长为4,E为AB上的点,且AE=1,O为AC的中点,P为BC上的动点,则△EOP周长的最小值是( )| A. | 4+3$\sqrt{2}$ | B. | $\sqrt{29}$+$\sqrt{5}$ | C. | 2+$\sqrt{5}$+3$\sqrt{2}$ | D. | $\sqrt{5}$+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
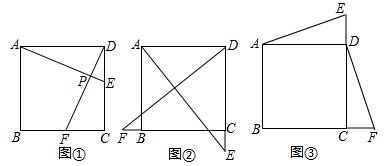
| 在数学课上,老师提出如下问题: 已知:Rt△ABC,∠ABC=90° 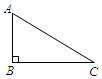 求作:矩形ABCD. |
①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=BO;③连接DA,DC.则四边形ABCD即为所求. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com