
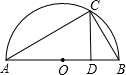
 如图,上面是半圆,下面是长方形,左、右两边分别割去两个半径相同的扇形,列出表示下列图形的面积的代数式,并化简.
如图,上面是半圆,下面是长方形,左、右两边分别割去两个半径相同的扇形,列出表示下列图形的面积的代数式,并化简. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 2×1 |
| 1 |
| 3 |
3×
|
| 8×8 |
| ab |
| a |
| b |
| ab |
| ab |
| ab |
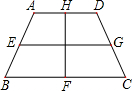
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
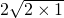 ; ②
; ②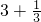 ______
______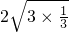 ③8+8______
③8+8______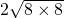
 ;
;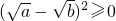 ,∴
,∴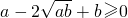 ,∴
,∴ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立. ,并指出等号成立时的条件.
,并指出等号成立时的条件.

查看答案和解析>>
科目:初中数学 来源:2009-2010学年江苏省无锡市育才中学九年级(上)期中数学试卷(解析版) 题型:解答题
 ; ②
; ② ______
______ ③8+8______
③8+8______
 ;
; ,∴
,∴ ,∴
,∴ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立. ,并指出等号成立时的条件.
,并指出等号成立时的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com