
分析 (1)设这个正多边形是n边形,根据n边形共有对角线$\frac{n(n-3)}{2}$条,即可列出方程:$\frac{n(n-3)}{2}$=35,求解即可;
(2)根据多边形的内角和为:(n-2)×180°,可求出其内角和.
解答 解:(1)设这个正多边形是n边形,根据题意得:
$\frac{n(n-3)}{2}$=35,
解得n1=10,n2=-7(不符题意,舍去).
故这个多边形是十边形;
(2)(10-2)×180°
=8×180°
=1440°.
故这个多边形内角和的度数是1440°.
点评 本题考查了多边形的对角线,多边形内角与外角.用到的知识点:n边形共有对角线$\frac{n(n-3)}{2}$条;多边形的内角和为:(n-2)×180°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
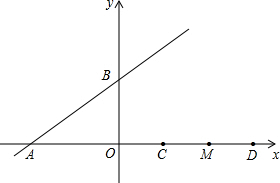 已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧)
已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 参赛者 | 答对题数 | 答错题数 | 得分 |
| A | 20 | 0 | 100 |
| B | 19 | 1 | 94 |
| C | 18 | 2 | 88 |
| D | 14 | 6 | 64 |
| E | 10 | 10 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com