
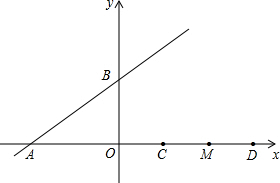
 已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧)
已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧)分析 (1)①利用待定系数法即可求得直线AB的解析式;
②根据相似三角形对应边成比例求得即可.
(2)作CE⊥CD,且CE=3,因为CD=4,根据勾股定理得出DE=5,所以sin∠CED=$\frac{4}{5}$,如果AB与x轴上方的优弧相交,交点为Q,根据同弧所对的圆周角相等,则∠CQD=∠CED,则sin∠CQD=$\frac{4}{5}$,当AB经过E点时,点E即为Q点,根据三角形相似求得OB的值为$\frac{3}{2}$,即可求得b的取值.
解答 解:(1)①∵直线AB经过点(4,6),
∴6=$\frac{3}{4}$×4+b,则b=3,
∴直线AB的解析式为y=$\frac{3}{4}$x+3.
②如图1,设点M到直线AB的距离为MN,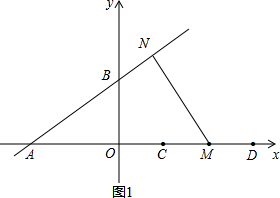 由直线AB的解析式为y=$\frac{3}{4}$x+3可知A(-4,0),B(0,3),
由直线AB的解析式为y=$\frac{3}{4}$x+3可知A(-4,0),B(0,3),
∴OA=4,OB=3,AB=5,
∵OD=6,点C,M是线段OD的三等分点,
∴AM=4+4=8,
∵∠BAO=∠MAN,∠AOB=∠ANM=90°,
∴△AOB∽△ANM,
∴$\frac{MN}{OB}$=$\frac{AM}{AB}$,
∴MN=$\frac{AM•OB}{AB}$=$\frac{8×3}{5}$=$\frac{24}{5}$.
(2)存在;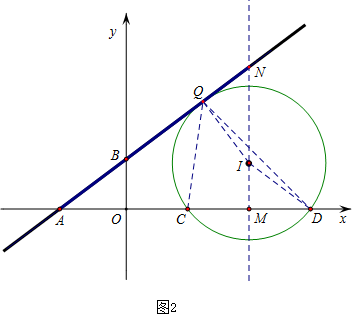
在CD的垂直平分线上取点I(4,1.5)
以I为圆心,ID为半径作圆,则⊙I必过点C,
在Rt△MID中,由勾股定理,得:
ID=$\sqrt{{2}^{2}+1.{5}^{2}}$=2.5,
sin∠MID=$\frac{MD}{ID}$=$\frac{4}{5}$,
当直线AB与⊙I相切(切点在第一象限)时,直线AB上存在唯一一个符合条件的点Q(切点),使得sin∠CQD=$\frac{4}{5}$(∠CQD=∠MID),此时设CD的垂直平分线交直线AB于点N,
在直线y=$\frac{3}{4}$x+b中,令y=0,则x=-$\frac{4}{3}$b,∴OA=$\frac{4}{3}$|b|,令x=0,则y=b,∴OB=|b|,
由勾股定理,得:AB=$\frac{5}{3}$|b|.
∵∠QNI=ABO,∠IQN=∠AOB=90°,
∴△IQN∽△AOB,
∴$\frac{IQ}{AO}$=$\frac{NI}{AB}$,$\frac{2.5}{\frac{4}{3}|b|}$=$\frac{NI}{\frac{5}{3}|b|}$,NI=$\frac{25}{8}$,
∴NM=$\frac{25}{8}$+$\frac{12}{8}$=$\frac{37}{8}$,N(4,$\frac{37}{8}$),
则把N(4,$\frac{37}{8}$)代入y=$\frac{3}{4}$x+b中,得:b=$\frac{13}{8}$,
此时直线AB的解析式为:y=$\frac{3}{4}$x+$\frac{13}{8}$.
若直线AB过点C,则把C(2,0)代入y=$\frac{3}{4}$x+b中,得:b=-$\frac{3}{2}$,
若直线AB过点D,则把D(6,0)代入y=$\frac{3}{4}$x+b中,得:b=-$\frac{9}{2}$,
∴当b>$\frac{13}{8}$或b≤-$\frac{9}{2}$时,点Q不存在;
当b=$\frac{13}{8}$或-$\frac{9}{2}$<b≤-$\frac{3}{2}$时,存在符合条件的一个点Q;
当-$\frac{3}{2}$<b<$\frac{13}{8}$时,存在符合条件的两个点Q.
点评 本题是一次函数的综合题,考查了待定系数法的应用,三角形相似的判定和直角三角函数等,(2)作出直角三角形CDE和三角形的外接圆是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
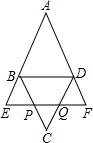 如图,四边形ABCD为平行四边形,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于E,F,且BE=BP,求证:
如图,四边形ABCD为平行四边形,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于E,F,且BE=BP,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
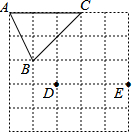 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com