
分析 x-$\frac{1}{x}$=3两边平方,得到x4+1=11x2,然后整体代入求值.
解答 解:(法一)由x-$\frac{1}{x}$=3,得(x-$\frac{1}{x}$)2=9
所以x2-2+$\frac{1}{{x}^{2}}$=9
即x2+$\frac{1}{{x}^{2}}$=11
所以$\frac{{x}^{4}+1}{{x}^{2}}=11$
所以5x4+5=55x2
所以原式=$\frac{54{x}^{2}}{2{x}^{2}}$
=27.
故答案为:27
(法二)$\frac{5{x}^{4}-{x}^{2}+5}{2{x}^{2}}$
=$\frac{5{x}^{4}+5}{2{x}^{2}}-\frac{1}{2}$
=$\frac{5}{2}({x}^{2}+\frac{1}{{x}^{2}})$-$\frac{1}{2}$
由x-$\frac{1}{x}$=3,得(x-$\frac{1}{x}$)2=9
即x2+$\frac{1}{{x}^{2}}$=11
所以原式=$\frac{5}{2}×11-\frac{1}{2}$
=27
故答案为:27
点评 本题考查了完全平方公式和分式的化简.运用整体代入的思想是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:图中平行于x轴的线段AB上的任意一点的坐标可表示为(x,-3)(-3≤x≤2).
已知:图中平行于x轴的线段AB上的任意一点的坐标可表示为(x,-3)(-3≤x≤2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
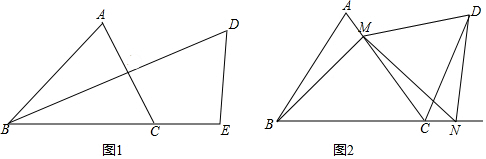
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点O为坐标原点,△ABC的顶点A在y轴的正半轴上,且OA=m,顶点B,C的坐标分别为(-m,0),(m,0),点D是线段AB上的一个动点(点D不与点A、B重合),点E是线段AC上的一点,且AE=BD,连接OD,DE,线段DE与线段OA相交于点F;
如图,在平面直角坐标系中,点O为坐标原点,△ABC的顶点A在y轴的正半轴上,且OA=m,顶点B,C的坐标分别为(-m,0),(m,0),点D是线段AB上的一个动点(点D不与点A、B重合),点E是线段AC上的一点,且AE=BD,连接OD,DE,线段DE与线段OA相交于点F;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我们给中国象棋棋盘建立一个平面直角坐标系如图是我市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),请以光岳楼为原点,画出直角坐标系,并用坐标表示下列景点的位置.
如图,我们给中国象棋棋盘建立一个平面直角坐标系如图是我市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度),请以光岳楼为原点,画出直角坐标系,并用坐标表示下列景点的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com