
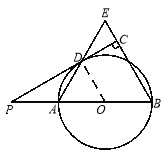
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.

(1)求证:AB=BE;
(2)连结OC,如果PD=![]() ,∠ABC=
,∠ABC=![]() ,求OC的长.
,求OC的长.
【答案】(1)证明过程见解析;(2)OC=![]()
【解析】
试题分析:(1)连接OD,根据OA=OD得出∠DAO=∠ADO,根据切线的性质得出PD⊥OD,从而说明OD∥BE,得出∠E=∠ADO,则∠E=∠DAO,从而说明答案;(2)根据OD∥BE,∠ABC=60°得出∠DOP=∠ABC=60°,根据tan∠DOP的值得出OD,OP和PB的长度,根据sin∠ABC的值得出PC和DC的长度,最后根据Rt△ODC的勾股定理求出OC的长度.
试题解析:(1)连结OD.
∵OA=OD,∴![]() ,
,
∵PD切⊙O于点D,∴PD⊥OD,
∵BE⊥PD, ∴OD∥BE,
∴![]() ,
,
∴![]() ,
,
∴AB=BE.
(2)∵OD∥BE,∠ABC=![]() ,
,
∴![]() ,
,
∵ PD⊥OD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() (舍负).
(舍负).



 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】下列命题中真命题有( )
①对角线互相平分且垂直的四边形是菱形;
②对角线互相平分且相等的四边形是菱形;
③对角线互相垂直且相等的四边形是菱形.
A.1个B.2个C.3个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提倡“绿色”出行,顺义区启动了公租自行车项目,为了解我区居民公租自行车的使用情况,某校的社团把使用情况分为A(经常租用)、B(偶尔租用)、C(不使用)三种情况.先后在2015年1月底和3月底做了两次调查,并根据调查结果绘制成了如下两幅不完整的统计图:

根据以上信息解答下列问题:
(1)在扇形统计图中,A(经常租用)所占的百分比是 ;
(2)求两次共抽样调查了多少人;并补全折线统计图;
(3)根据调查的结果,请你谈谈从2015年1月底到2015年3月底,我区居民使用公租自行车的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题:

(1)该校共有 名学生;
(2)在图1中,“三等奖”随对应扇形的圆心角度数是 ;
(3)将图2补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com