
科目:初中数学 来源:不详 题型:解答题
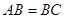 ,且
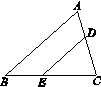
,且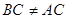 ),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).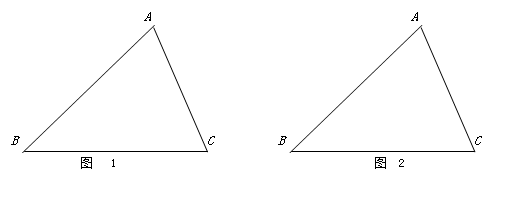 (1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
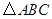 中,
中,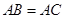 ,点
,点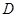 为
为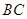 边的中点,点
边的中点,点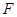 在
在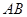 上,连结
上,连结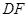 并延长到点
并延长到点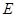 ,使
,使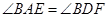 ,点
,点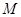 在线段
在线段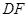 上,且
上,且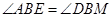 .
.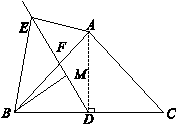
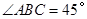 时,求证:
时,求证: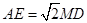 ;
;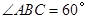 时,则线段
时,则线段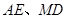 之间的数量关系为 ;
之间的数量关系为 ;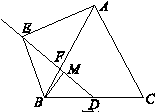
 2)的条件下,延长
2)的条件下,延长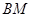 到
到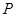 ,使
,使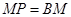 ,连接
,连接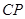 ,若
,若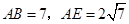 ,求
,求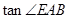 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
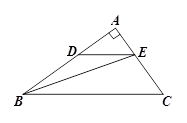
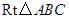 中,
中,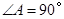 ,
,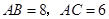 .若动点
.若动点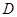 从点
从点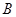 出发,沿线段
出发,沿线段 运动到点
运动到点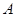 为止,运动速度为每秒2个单位长度.过点
为止,运动速度为每秒2个单位长度.过点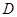 作
作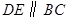 交
交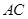 于点
于点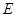 ,设动点
,设动点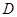 运动的时间为
运动的时间为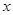 秒,
秒,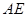 的长为
的长为 .
.
 关于
关于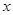 的函数关系式,并写出自变量
的函数关系式,并写出自变量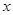 的取值范围;
的取值范围;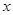 为何值时,
为何值时,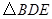 的面积
的面积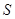 有最大值,最大值为多少?
有最大值,最大值为多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
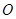 为等腰直角三角形
为等腰直角三角形 的重心,
的重心,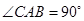 ,直线
,直线 过点
过点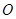 ,过
,过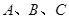 三点分别作直线
三点分别作直线 的垂线,垂足分别为点
的垂线,垂足分别为点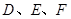 .
.  与
与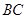 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段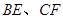 和
和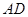 三者之间的数量关系并证明;
三者之间的数量关系并证明; 绕点
绕点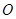 旋转到与
旋转到与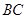 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段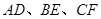 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.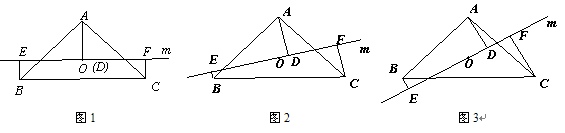
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(4,2) | B.(4,4) | C.(4,5) | D.(5,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com