
如图, 射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心, cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 .(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 .(单位:秒)

t=2或3≤t≤7或t=8.
【解析】
试题分析:求出AB=AC=BC=4cm,MN=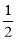 AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;
试题解析:∵△ABC是等边三角形,
∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.
∴N为BC中点,
∴MN=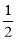 AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
分为三种情况:①如图1
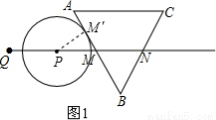
当⊙P切AB于M′时,连接PM′,
则PM′=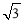 cm,∠PM′M=90°,
cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,
∴M′M=1cm,PM=2MM′=2cm,
∴QP=4cm-2cm=2cm,
即t=2;
②如图2,
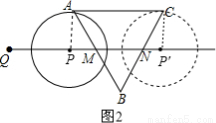
当⊙P于AC切于A点时,连接PA,
则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=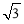 cm,
cm,
∴PM=1cm,
∴QP=4cm-1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=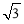 cm,
cm,
∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,
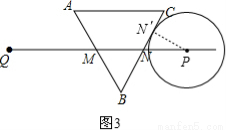
当⊙P切BC于N′时,连接PN′
则PN′=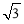 cm,∠PN′N=90°,
cm,∠PN′N=90°,
∵∠PNN′=∠BNM=60°,
∴N′N=1cm,PN=2NN′=2cm,
∴QP=4cm+2cm+2cm=8cm,
即t=8.
考点:1.切线的性质;2.等边三角形的性质.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源:2013-2014学年江苏省淮安市洪泽县九年级中考二模数学试卷(解析版) 题型:选择题
已知三角形三边的长分别为4、5、x,则x不可能是( )
A.3 B.5 C.7 D.9
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市要塞片九年级下学期期中考试数学试卷(解析版) 题型:选择题
2011年3月11日,日本大地震举世关注,小明上网搜索“日本大地震”获得约7 940 000条结果,数据“7 940 000”用科学记数法表示应为( )
A.79.4×104 B.7.94×106 C.7.94×105 D. 79.4×105
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:解答题
某市“每天锻炼一小时,幸福生活一辈子”活动已开展了一年,为了了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A.从一个社区随机选取200名居民;
B.从一个城镇的不同住宅楼中随机选取200名居民;
C.从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象,然后进行调查.
(1)在上述调查方式中,你认为比较合理的一个是_______(填序号).
(2)由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图,在这个调查中,200名居民每天锻炼2小时的人数是多少?
(3)若该市有100万人,则请你利用(2)中的调查结果,估计该市每天锻炼2小时及以上的人数.
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:选择题
关于x的一元二次方程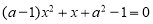 的一个根0,则a值为 ( )
的一个根0,则a值为 ( )
A.1B.-1C±1D.0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级下学期期中考试数学试卷(解析版) 题型:填空题
如图,A、B是反比例函数y= 上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,S四边形ABDC=9,则k= .
OC,S四边形ABDC=9,则k= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com