
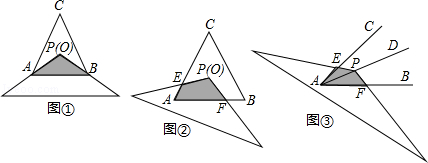
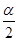 的三角函数值表示)
的三角函数值表示) ;
;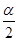 cos
cos .
.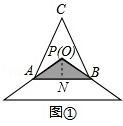

 .
. .
. ;
;

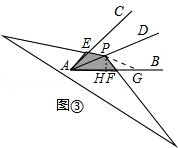
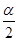 .
.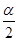 .
.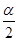 ,AH=2cos
,AH=2cos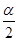 .
.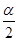 .
.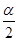 cos
cos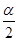 .
.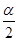 cos
cos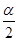 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源:不详 题型:解答题
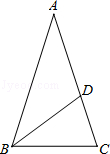
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距18
里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距18| 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
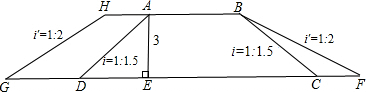 GH、BF斜坡的坡度i'=1:2,若路长为10000米,则加宽的土石方量共是______立方米.
GH、BF斜坡的坡度i'=1:2,若路长为10000米,则加宽的土石方量共是______立方米.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.30m | B.30tan75m |
| C.30cot75°m | D.30(tan75°-tan35°)m |
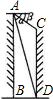
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
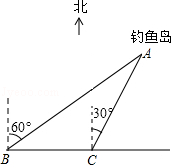
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com