
 如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.
如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.分析 (1)作PE⊥x轴于点E,可得PE=4,根据面积公式计算可得;
(2)由S△BOP=3S△AOP可得OB=3OA,即B(6,0),再根据P(a,4)在直线y=2x上求得点P的坐标,最后利用待定系数法求解可得直线BD的解析式.
解答 解:(1)作PE⊥x轴于点E,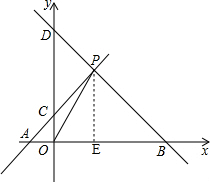
∵点P(a,4),则PE=4,
∴S△AOP=$\frac{1}{2}$OA•PE=$\frac{1}{2}$×2×4=4;
(2)∵S△BOP=3S△AOP,
∴OB=3OA,
∴点B坐标为(6,0),
又∵点P(a,4)在直线y=2x上,
∴2a=4,a=2,
∴P(2,4),
设直线BD解析式为y=kx+b,
则$\left\{\begin{array}{l}{2k+b=4}\\{6k+b=0}\end{array}\right.$,
解得:k=-1、b=6,
∴直线BD的解析式为y=-x+6.
点评 本题考查了待定系数法求函数解析式及三角形的面积、两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.


科目:初中数学 来源: 题型:填空题
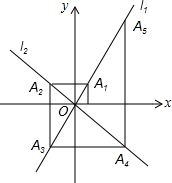 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2007的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2007的坐标为(21008,21009).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
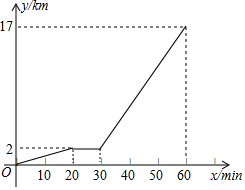 星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:
星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
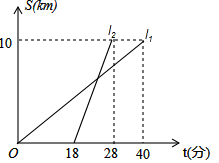 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的有( )
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.186×103 | B. | 3.186×104 | C. | 31.86×102 | D. | 0.3186×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
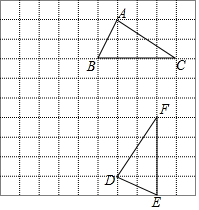 如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形完成下列问题.
如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形完成下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com