
【题目】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将线段
,将线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,连接
,连接![]() ,
,![]() ,构成平行四边形
,构成平行四边形![]() .
.
(1)请写出点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上任意一个点(不与
上任意一个点(不与![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() ,试探索
,试探索![]() 、
、![]() 、
、![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.

科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.
(1)a=___,b=___,△BCD的面积为______;
(2)如图2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;
(3)如图3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,
![]() 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.
②![]() 59319的个位数是9,又
59319的个位数是9,又![]() ,
,
![]() 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①![]() ;
;
②![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 ![]() 可化为3x=6.
可化为3x=6.
D.方程 ![]() 系数化为1,得x=﹣1
系数化为1,得x=﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() = .
= .
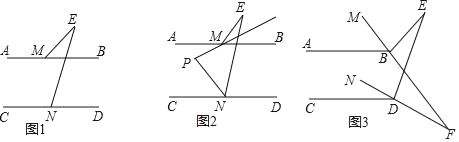
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们提供如下定理:在直角三角形中,30°的锐角所对的直角边是斜边的一半,
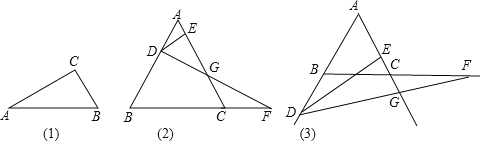
如图(1),Rt△ABC中,∠C=90°,∠A=30°,则BC=![]() AB.
AB.
请利用以上定理及有关知识,解决下列问题:
如图(2),边长为6的等边三角形ABC中,点D从A出发,沿射线AB方向有A向B运动点F同时从C出发,以相同的速度沿着射线BC方向运动,过点D作DE⊥AC,DF交射线AC于点G.
(1)当点D运动到AB的中点时,直接写出AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图3的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A 在 y 轴正半轴上点 B 在 x 轴负半轴上,且 AB=2,∠BAO=15°,点 P 是线段OA 上的一个动点,则 PB ![]() PA 的最小值为_____________.
PA 的最小值为_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com