
【题目】如图,抛物线 ![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
【答案】
(1)解:∵抛物线 ![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),
∴  ,
,
解得:  ,
,
∴抛物线的解析式是 ![]()
(2)解:∵ ![]() =
= ![]() ,
,
∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1
(3)解:存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时 ![]() =
= ![]() ,
,
解得,y= ![]() ,
,
即点P的坐标为(1, ![]() );
);
②当DA=DP时, ![]() =
= ![]() ,
,
解得,y= ![]() ,
,
即点P的坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
③当AD=AP时, ![]() =
= ![]() ,
,
解得,y=±4,
即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
【解析】(1)根据题意得一个三元一次方程组,解之即可得抛物线解析式.
(2)根据(1)中得出的解析式,配成顶点式,从而得出顶点式和对称轴.
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:①当PA=PD时,②当DA=DP时,③当AD=AP时,根据两点间距离公式计算即可得出P点坐标.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,则该运动员此次掷铅球的成绩是( )
,则该运动员此次掷铅球的成绩是( )
A.6m
B.12m
C.8m
D.10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5.
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位认真开展学习和实践科学发展观活动,在阶段总结中提出对本单位今后的整改措施,并在征求职工对整改方案的满意程度时进行民主测评,测评等级为:很满意、较满意、满意、不满意四个等级.

(1)若测评后结果如扇形图(图①),且测试等级为很满意、较满意、满意、不满意的人数之比为2:5:4:1,则图中a= ° ,β= °.
(2)若测试后部分统计结果如直方图(图②),请将直方图补画完整,并求出该单位职工总人数为 人.
(3)按上级要求,满意度必须不少于95%方案才能通过,否则,必须对方案进行完善.若要使该方案完善后能获得通过,至少还需增加 人对该方案的测评等级达满意(含满意)以上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将线段
,将线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,连接
,连接![]() ,
,![]() ,构成平行四边形
,构成平行四边形![]() .
.
(1)请写出点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上任意一个点(不与
上任意一个点(不与![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() ,试探索
,试探索![]() 、
、![]() 、
、![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图6,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时后到达C点,总共航行了208千米,已知水流的速度是2千米/时。
(1)求游艇在静水中的速度。
(2)由于AC段在建桥,游艇用同样的速度沿原路返回共需多少时间?(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
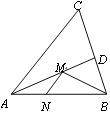
【题目】如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠B、∠D的两边分别平行.
(1)在图1中, ∠B与∠D的数量关系是 ;
(2)在图2中, ∠B与∠D的数量关系是 ;
(3)用一句话归纳的结论为
(4)应用:若两个角的两边分别互相平行,其中一个角比另一个角的2倍小30°,求着两个角的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com