
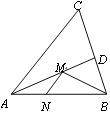
【题目】如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是__________.
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABCD= ![]() AM2.
AM2.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() = .
= .
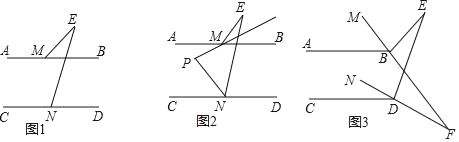
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中正确的是( ).①小明家和学校距离1200米;②小华乘坐公共汽车的速度是240米/分;③小华乘坐公共汽车后7:50与小明相遇;④小华的出发时间不变,当小华由乘公共汽车变为跑步,且跑步的速度是100米/分时,他们可以同时到达学校.

A. ①③④B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们提供如下定理:在直角三角形中,30°的锐角所对的直角边是斜边的一半,
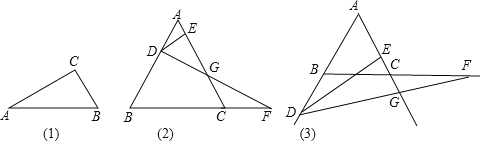
如图(1),Rt△ABC中,∠C=90°,∠A=30°,则BC=![]() AB.
AB.
请利用以上定理及有关知识,解决下列问题:
如图(2),边长为6的等边三角形ABC中,点D从A出发,沿射线AB方向有A向B运动点F同时从C出发,以相同的速度沿着射线BC方向运动,过点D作DE⊥AC,DF交射线AC于点G.
(1)当点D运动到AB的中点时,直接写出AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图3的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)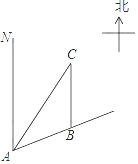
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过四边形的一个顶点可以画一条对角线,且把四边形分成两个三角形;过五边形的一个顶点可以画两条对角线,且把五边形分成三个三角形;......猜想:过n边形的一个顶点可以画_________条对角线,且把n边形分成 _________个三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com