
【题目】如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点A处测得码头C在船的东北方向,航行40分钟后到达B处,这时码头C恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头C的最近距离.(结果精确到0.1海里,参考数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)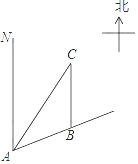
【答案】解:过点C作CE⊥AB于点E,过点B作BD⊥AC于点D,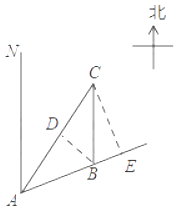
由题意可知:船在航行过程中与码头C的最近距离是CE,
AB=30× ![]() =20,
=20,
∵∠NAC=45°,∠NAB=75°,
∴∠DAB=30°,
∴BD= ![]() AB=10,
AB=10,
由勾股定理可知:AD=10 ![]()
∵BC∥AN,
∴∠BCD=45°,
∴CD=BD=10,
∴AC=10 ![]() +10
+10
∵∠DAB=30°,
∴CE= ![]() AC=5
AC=5 ![]() +5≈13.7
+5≈13.7
答:船在航行过程中与码头C的最近距离是13.7海里
【解析】根据题意得到AB的值,再根据在直角三角形中,30度角所对的边是斜边的一半和勾股定理,求出AD的值,得到CE的值.
【考点精析】本题主要考查了关于方向角问题的相关知识点,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能正确解答此题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,则接收方对应收到的密码为A,B,C.双方约定:A=2a﹣b,B=2b,C=b+c,例如发出1,2,3,则收到0,4,5.
(1)当发送方发出一组密码为2,3,5时,则接收方收到的密码是多少?
(2)当接收方收到一组密码2,8,11时,则发送方发出的密码是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
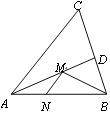
【题目】如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道![]() 有以下两个方案:
有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最![]() 短在途中标出M、N的位置,保留画图痕迹;
短在途中标出M、N的位置,保留画图痕迹;

设方案一中铺设的支管道总长度为L1![]() ,方案二中铺设的支管道总长度为
,方案二中铺设的支管道总长度为![]() ,则L1与L2的大小关系为: L1_____ L2(填
,则L1与L2的大小关系为: L1_____ L2(填![]() ”、
”、![]() ”或)理由是______.
”或)理由是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①![]()
②![]()
③x(x+1)-(x-1)(x+1).
④用简便方法计算:20192-2018×2020
⑤先化简,再求值:当x=﹣2,y=3时,求代数式(y+3x)(3x-y)-(3y-x)(3y+x)的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠B、∠D的两边分别平行.
(1)在图1中, ∠B与∠D的数量关系是 ;
(2)在图2中, ∠B与∠D的数量关系是 ;
(3)用一句话归纳的结论为
(4)应用:若两个角的两边分别互相平行,其中一个角比另一个角的2倍小30°,求着两个角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com