
ЁОЬтФПЁПЁОдФЖСаТжЊЁП
Ш§НЧаЮжаШЮКЮвЛБпЕФЦНЗНЕШгкЦфЫќСНБпЕФЦНЗНЕФКЭМѕШЅетСНБпгыЫќУЧЕФМаНЧЕФгрЯвЕФЛ§ЕФСНБЖЃЎ
МДЃКШчЭМ1ЃЌ.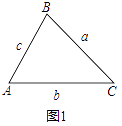
дкЁїABCжаЃЌвбжЊAB=cЃЌBC=aЃЌCA=bЃЌдђгаЃК
a2=b2+c2Љ2bccosAЃЌb2=a2+c2Љ2accosBЃЌc2=a2+b2Љ2abcosC
РћгУетИіе§ШЗНсТлПЩЧѓНтЯТСаЮЪЬтЃК
Р§дкЁїABCжаЃЌвбжЊa=2 ![]() ЃЌb=2
ЃЌb=2 ![]() ЃЌc=
ЃЌc= ![]() ЃЌЧѓЁЯAЃЎ
ЃЌЧѓЁЯAЃЎ
НтЃКЁпa2=b2+c2Љ2bccosAЃЌ
cosA= ![]() =
= ![]() =
= ![]() ЃЎ
ЃЎ
ЁрЁЯA=60ЁуЃЎ
ЁОгІгУаТжЊЁП
ЃЈ1ЃЉбЁдёЬтЃКдкЁїABCжаЃЌвбжЊb=ccosAЃЌa=csinBЃЌФЧУДЁїABCЪЧЃЈ ЃЉЃЎ
A.ЕШБпШ§НЧаЮ
B.ЕШбќШ§НЧаЮ
C.ЕШбќжБНЧШ§НЧаЮ
D.жБНЧШ§НЧаЮ
ЃЈ2ЃЉШчЭМ2ЃЌ
ФГПЭТждкAДІПДИлПкDдкПЭТжЕФББЦЋЖЋ50ЁуЃЌAДІПДЕЦЫўBдкПЭТжЕФББЦЋЮї30ЁуЃЌОрРыЮЊ2 ![]() КЃРяЃЌПЭТжгЩAДІЯђе§ББЗНЯђКНааЕНCДІЪБЃЌдйПДИлПкDдкПЭТжЕФФЯЦЋЖЋ80ЁуЃЌОрРыЮЊ6КЃРяЃЎЧѓДЫЪБCДІЕНЕЦЫўBЕФОрРыЃЎ
КЃРяЃЌПЭТжгЩAДІЯђе§ББЗНЯђКНааЕНCДІЪБЃЌдйПДИлПкDдкПЭТжЕФФЯЦЋЖЋ80ЁуЃЌОрРыЮЊ6КЃРяЃЎЧѓДЫЪБCДІЕНЕЦЫўBЕФОрРыЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉC
ЃЈ2ЃЉ
ЁЯADC=180ЁуЉ80ЁуЉ50Ёу=50ЁуЃЌ
ЁрCA=CD=6ЃЌ
BC2=AB2+AC2Љ2ABACcosЁЯBAC=ЃЈ2 ![]() ЃЉ2+62Љ2ЁС3
ЃЉ2+62Љ2ЁС3 ![]() ЁС6ЁС
ЁС6ЁС ![]() =12ЃЌ
=12ЃЌ
ЁрBC=2 ![]() ЃЌ
ЃЌ
Д№ЃКCДІЕНЕЦЫўBЕФОрРыЮЊ2 ![]() КЃРя
КЃРя
ЁОНтЮіЁПНтЃКЃЈ1ЃЉЁпb=ccosAЃЌa=csinBЃЌ
ЁрcosA= ![]() ЃЌsinB=
ЃЌsinB= ![]() ЃЌ
ЃЌ
Ёрa2=b2+c2Љ2bccosA=b2+c2Љ2bcЁС ![]() =b2Љc2 ЃЌ
=b2Љc2 ЃЌ
Ёрa2+c2=b2 ЃЌ
ЁрЁїABCЪЧжБНЧШ§НЧаЮЃЌЁЯB=90ЁуЃЌ
Ёрa=csinB=cЃЌ
ЁрЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЙЪбЁЃКCЃЎ
ЁОПМЕуОЋЮіЁПЙигкБОЬтПМВщЕФЙигкЗНЯђНЧЮЪЬтЃЌашвЊСЫНтжИББЛђжИФЯЗНЯђЯпгыФПБъЗНЯђ ЯпЫљГЩЕФаЁгк90ЁуЕФЫЎЦННЧЃЌНазіЗНЯђНЧВХФмЕУГіе§ШЗД№АИЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЁбOЕФФкНгЫФБпаЮЃЌЁЯB=135ЁуЃЌдђЁЯAOCЕФЖШЪ§ЮЊЃЈ ЃЉ 
A.45Ёу
B.90Ёу
C.100Ёу
D.135Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
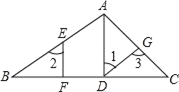
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCЃЌДЙзуЮЊDЃЌЕуEдкABЩЯЃЌEFЁЭBCЃЌДЙзуЮЊFЃЎ
(1)ADгыEFЦНааТ№ЃПЮЊЪВУДЃП
(2)ШчЙћЁЯ1ЃНЁЯ2ЃЌЧвЁЯ3ЃН115ЁуЃЌЧѓЁЯBACЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌADЪЧЁїABCЕФжаЯпЃЌЁЯACEЪЧЁїABCЕФЭтНЧЃЎ 
ЃЈ1ЃЉЖСЯТСагяОфЃЌГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЎ ЂйзїЁЯACEЕФНЧЦНЗжЯпЃЌНЛBAбгГЄЯпгкЕуFЃЛ
ЂкЙ§ЕуDзїDHЁЮACЃЌНЛABгкЕуHЃЌСЌНгCHЃЎ
ЃЈ2ЃЉвРОнвдЩЯЬѕМўЃЌНтД№ЯТСаЮЪЬтЃЎ ЂйгыЁїAHDУцЛ§ЯрЕШЕФШ§НЧаЮЪЧЃЛ
ЂкШєЁЯB=40ЁуЃЌЁЯF=30ЁуЃЌЧѓЁЯBACЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжВЪїНкЦкМфЃЌФГЕЅЮЛгћЙКНјAЁЂBСНжжЪїУчЃЌШєЙКНјAжжЪїУч3ПУЃЌBжжЪїУч5ПУЃЌаш2100дЊЃЌШєЙКНјAжжЪїУч4ПУЃЌBжжЪїУч10ПУЃЌаш3800дЊЃЎ
ЃЈ1ЃЉЧѓЙКНјAЁЂBСНжжЪїУчЕФЕЅМлЃЛ
ЃЈ2ЃЉШєИУЕЅЮЛзМБИгУВЛЖргк8000дЊЕФЧЎЙКНјетСНжжЪїУчЙВ30ПУЃЌЧѓAжжЪїУчжСЩйашЙКНјЖрЩйПУЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЬтЮФЃЉШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌDCЁЮABЃЌAD=BCЃЌBDЦНЗжЁЯABCЃЎ

ЃЈ1ЃЉЧѓжЄЃКAD=DCЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЩЯЪіЬѕМўЯТЃЌШєЁЯA=ЁЯABC=60ЁуЃЌЙ§ЕуDзїDEЁЭABЃЌЙ§ЕуCзїCFЁЭBDЃЌДЙзуЗжБ№ЮЊEЁЂFЃЌСЌНгEFЃЎХаЖЯЁїDEFЕФаЮзДВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНОПЬтЃКШчЭМЃЌдкЕШбќШ§НЧаЮABCжаЃЌABЃНACЃЌЦфЕзБпГЄЮЊ8 cmЃЌбќГЄЮЊ5 cmЃЌвЛЖЏЕуPдкЕзБпЩЯДгЕуBГіЗЂЯђЕуCвд0.25 cm/sЕФЫйЖШвЦЖЏЃЌЧыФуЬНОПЃКЕБЕуPдЫЖЏЖрГЄЪБМфЪБЃЌЕуPгыЖЅЕуAЕФСЌЯпPAгыбќДЙжБЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГНЬг§ЭјеОЖдЯТдизЪдДЙцЖЈШчЯТЃКШєзЂВсVIPгУЛЇЃЌдђЯТдиУПЗнзЪдДЪе![]() дЊЃЌСэЭтУПФъЪе500дЊЕФVIPЛсдБЗбЃЌШєзЂВсЦеЭЈгУЛЇЃЌдђЯТдиУПЗнзЪдДЪе
дЊЃЌСэЭтУПФъЪе500дЊЕФVIPЛсдБЗбЃЌШєзЂВсЦеЭЈгУЛЇЃЌдђЯТдиУПЗнзЪдДЪе![]() дЊЃЌВЛЪеЦфЫќЗбгУ
дЊЃЌВЛЪеЦфЫќЗбгУ
![]() ЗжБ№аДГізЂВсVIPгУЛЇЕФЪеЗб
ЗжБ№аДГізЂВсVIPгУЛЇЕФЪеЗб![]() дЊ
дЊ![]() КЭзЂВсЦеЭЈгУЛЇ
КЭзЂВсЦеЭЈгУЛЇ![]() дЊ
дЊ![]() гыЯТдиЪ§СП
гыЯТдиЪ§СП![]() Зн
Зн![]() жЎМфЕФКЏЪ§ЙиЯЕЪН
жЎМфЕФКЏЪ§ЙиЯЕЪН
![]() ФГбЇаЃУПФъвЊЯТди1500ЗнзЪдДЃЌФЧУДзЂВсФФжжгУЛЇБШНЯКЯЫуЃП
ФГбЇаЃУПФъвЊЯТди1500ЗнзЪдДЃЌФЧУДзЂВсФФжжгУЛЇБШНЯКЯЫуЃП
![]() вЛФъФкЯТдиЖрЩйЗнзЪдДЪЧСНжжгУЛЇЪеЗбвЛбљЃП
вЛФъФкЯТдиЖрЩйЗнзЪдДЪЧСНжжгУЛЇЪеЗбвЛбљЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ ABCD жаЃЌABЁЭADЃЌBCЁЭDCЃЌЕу MЁЂN ЗжБ№ЪЧ ABЁЂBC БпЩЯЕФЖЏЕуЃЌЁЯBЃН56ЁуЃЎЕБЁїDMN ЕФжмГЄзюаЁЪБЃЌдђЁЯMDN ЕФЖШЪ§ЪЧ_____

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com