
【题目】如图,四边形 ABCD 中,AB⊥AD,BC⊥DC,点 M、N 分别是 AB、BC 边上的动点,∠B=56°.当△DMN 的周长最小时,则∠MDN 的度数是_____

【答案】68°.
【解析】
延长DA至E点,使AD=AE,延长DC至F点,使CD=CF,可得E、N、M、F在同一直线上时△DMN 的周长最小,可得∠MDN的值.
解:如图: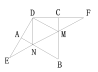
延长DA至E点,使AD=AE,又AB⊥AD,可得点D和E关于AB对称;
延长DC至F点,使CD=CF,又BC⊥DC,可得D和F关于CB对称,
连接EF,此时与AB、BC的交点N、M即为所求,连接DN、DM,
则:DN=EN,DM=MF,![]() ∠E=∠EDN, ∠E =∠FDM;
∠E=∠EDN, ∠E =∠FDM;
在四边形ABCD中,AB⊥AD,BC⊥DC,∠B=56°,
易得∠ADC=180°-56°=124°,
![]() 在△DEF中, ∠E+∠F=180°-∠ADC=56°,
在△DEF中, ∠E+∠F=180°-∠ADC=56°,
即∠EDN+∠FDM=56°,
![]() ∠MDN=∠ADC-(∠EDN+∠FDM)=124°-56°=68°,
∠MDN=∠ADC-(∠EDN+∠FDM)=124°-56°=68°,
故答案:68°.


科目:初中数学 来源: 题型:
【题目】【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.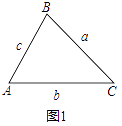
在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2 ![]() ,b=2
,b=2 ![]() ,c=
,c= ![]() ,求∠A.
,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA= ![]() =
= ![]() =
= ![]() .
.
∴∠A=60°.
【应用新知】
(1)选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
(2)如图2,
某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2 ![]() 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )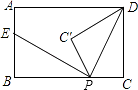
A.
B. 
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
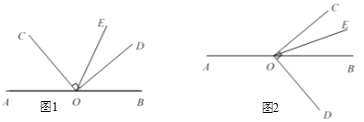
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:![]() -
-![]() =1-
=1-![]()
解:去分母,得_________________________________.
去括号,得___________________________.
移项,得___________________________.
合并同类项,得__________.
两边都除以______,得x=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
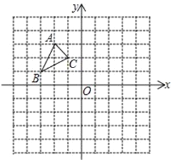
【题目】如图,△ABC 中,A(-2,3)、B(-3,1)、C(-1,2)
(1)作△ABC 关于直线 x=1 对称的图形△A1B1C1,写出三顶点 A1、B1、C1的坐标
(2)在 x 轴上求作一点 D,使四边形 ABDC 的周长最小(保留作图痕迹,不要求写作法和证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 a、b、c 为△ABC 的三边,且满足 a2+b2+c2=ab+ac+bc.点 D 是 AC边的中点,以点 D 为顶点作∠FDE=120°,角的两边分别与直线 AB 和 BC 相交于点 F 和点 E
(1)试判断△ABC 的形状,说明理由
(2)如图 1,将△ABC 图形中∠FDE=120°绕顶点 D 旋转,当两边 DF、DE 分别与边 AB 和射线BC 相交于点 F、E 时,三线段 BE、BF、AB 之间存在什么关系?证明你的结论
(3)如图 2,当角两边 DF、DE 分别与射线 AB 和射线 BC 相交两点 F、E 时,三线段 BE、BF、AB 之间存在什么关系

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知双曲线y= ![]() (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ![]() ≤k′x;
≤k′x;
(2)如图2,过原点O作另一条直线l,交双曲线y= ![]() (k>0)于P,Q两点,点P在第一象限.
(k>0)于P,Q两点,点P在第一象限.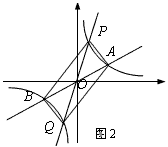
四边形APBQ一定是;
(3)若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
(4)设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求三次传球后,球回到甲脚下的概率;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com