【题目】如图，等腰梯形MNPQ的上底长为2，腰长为3，一个底角为60°．正△ABC的边长为1，它的一边AC在MN上，且顶点A与M重合．现将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚，翻滚到有一个顶点与Q重合即停止滚动．

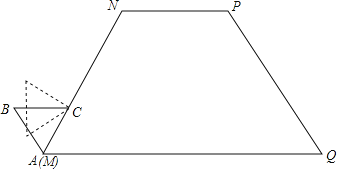
（1）请在所给的图中，画出顶点A在正△ABC整个翻滚过程中所经过的路线图；

（2）求正△ABC在整个翻滚过程中顶点A所经过的路径长；

（3）求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S．

参考答案：

【答案】（1）画图见解析；（2）点A所经过的路线长π；（3）π+．

【解析】

试题分析：（1）根据将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚翻滚到有一个顶点与Q重合即停止滚动，转动过程中始终是以半径为1的弧，据此画出圆弧即可．

（2）根据翻滚路线结合弧长公式求出即可；

（3）根据总结的翻转角度和翻转半径，求出圆弧与梯形的边长围成的扇形的面积即可．

解：（1）如图所示：

（2）点A所经过的路线长：×4+=π；

（3）如图所示：

根据正三角形边长为1，则高AD为：cos30°=，则AD=，

故面积为：×1×，

围成的图形的面积：3个圆心角为120°的扇形+2个正三角形的面积+一个半圆面积，

（根据要求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S，则最后一段弧没有和PQ围成闭合的图形，故可以不求这部分面积）

所以点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S为：

×π×12+2×1×+3×=π+．

关闭