【题目】一次函数y=kx+4的图象经过点（3，﹣2）
（1）求这个函数解析式；
（2）在下面方格图中画出这个函数的图象．
【答案】解：（1）∵一次函数y=kx+4的图象经过点 （3，﹣2）
∴﹣2=3k+4
解得：k=﹣2
∴一次函数的解析式是y=﹣2x+4；
（2）∵一次函数的解析式是y=﹣2x+4
令x=0，得y=4
令y=0，得x=2，
x | … | 0 | 2 | … |
y=﹣2x+4 | … | 4 | 0 | … |
画出函数的图象如图：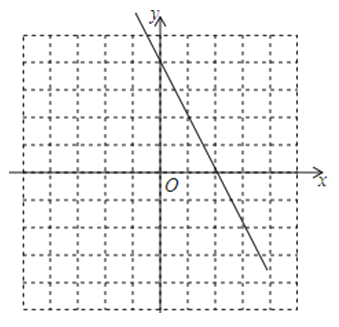
【解析】（1）把点（3，﹣2）代入y=kx+4，即可求出k的值．
（2）利用两点法画出图象即可．
【考点精析】利用一次函数的图象和性质和确定一次函数的表达式对题目进行判断即可得到答案，需要熟知一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法．
科目：初中数学 来源： 题型：
【题目】（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低，若该果园每棵果树产果y千克，增种果树x棵，它们之间的函数关系如图所示．
(1)求y与x之间的函数解析式；
(2)在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？
(3)当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图坐标系中，O(0，0) ，A(6，6
)，B(12，0)．将△OAB沿直线CD折叠，使点A恰好落在线段OB上的点E处，若OE＝
，则CE : DE的值是______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
