
【题目】甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图像,解答下列问题: 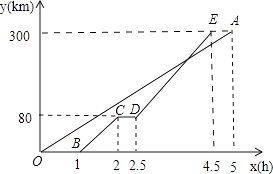
(1)线段CD表示轿车在中途停留了h;
(2)求轿车从甲地出发后经过多长时间追上货车.
【答案】
(1)0.5
(2)解:设过点D(2.5,80),点E(4.5,300)的直线解析式为:y=kx+b,
则 ![]()
解得, ![]()
∴过DE的直线解析式为:y=110x﹣195,
设过点O(0,0),A(5,300)的直线的解析式为y=mx,
则5m=300,得m=60,
即过点O、A的直线的解析式为:y=60x,
![]()
解得,x=3.9,
3.9﹣1=2.9h,
即轿车从甲地出发后经过2.9h追上货车
【解析】解:(1)由图像可知, 线段CD表示轿车在中途停留的时间是:2.5﹣2=0.5h,
故答案为:0.5;
(1)根据函数图像可以得到轿车在中途停留的时间;(2)由图像可知,两车相遇在轿车行驶的DE段,只要求出直线DE的解析式和直线OA的解析式,联立方程组即可求得相遇时间,用相遇的时间﹣轿车晚行驶的1小时,即可求得轿车从甲地出发后经过多长时间追上货车.


科目:初中数学 来源: 题型:
【题目】如图, ![]() 是线段
是线段![]() 上一点,
上一点, ![]() ,
, ![]() .
.
![]()
(![]() )
)![]() __________
__________ ![]() ;
;
(![]() )动点
)动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度沿
的速度沿![]() 向右运动,终点为
向右运动,终点为![]() ;点
;点![]() 以
以![]() 的速度沿
的速度沿![]() 向左运动,终点为
向左运动,终点为![]() .当一个点到达终点,另一个点也随之停止运动.求运动多少秒时,
.当一个点到达终点,另一个点也随之停止运动.求运动多少秒时, ![]() 、
、![]() 、
、![]() 三点,有一点恰好是以另两点为端点的线段的中点?
三点,有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考( )
A. 众数 B. 平均数 C. 加权平均数 D. 中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积? 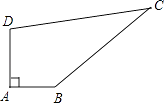
查看答案和解析>>
科目:初中数学 来源: 题型:
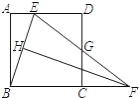
【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
(1)过点F作FH⊥BE于点H,证明:![]() ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com