
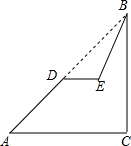
 如图,已知斜坡AB长为60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为$\sqrt{3}$:1,求休闲平台DE的长是多少米?(结果保留根号).
如图,已知斜坡AB长为60$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为$\sqrt{3}$:1,求休闲平台DE的长是多少米?(结果保留根号). 分析 由三角函数的定义,即可求得DF与BF的长,又由坡度的定义,即可求得EF的长,继而求得休闲平台DE的长.
解答 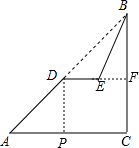 解:作DP⊥AC,垂足为点P,延长DE交BC于点F,
解:作DP⊥AC,垂足为点P,延长DE交BC于点F,
∵FM∥CG,
∴∠BDF=∠BAC=45°,
∵斜坡AB长60$\sqrt{2}$米,D是AB的中点,
∴BD=30$\sqrt{2}$米,
∴DF=BD•cos∠BDF=30$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=30(米),BF=DF=30米,
∵斜坡BE的坡比为$\sqrt{3}$:1,
∴$\frac{BF}{EF}$=$\frac{\sqrt{3}}{1}$,
解得:EF=10$\sqrt{3}$(米),
∴DE=DF-EF=30-10$\sqrt{3}$(米).
答:休闲平台DE的长是(30-10$\sqrt{3}$)米;
点评 此题考查了坡度坡角问题以及俯角仰角的定义.此题难度较大,注意根据题意构造直角三角形,并解直角三角形;注意掌握数形结合思想与方程思想的应用.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
 阅读理解
阅读理解查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 方差 | D. | 众数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 是原来的20倍 | B. | 是原来的10倍 | C. | 是原来的0.1倍 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com