



 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:044
填入推理的依据及过程.
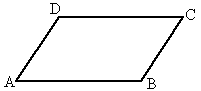
已知:如图AB∥CD,AD∥BC.
求证:∠A=∠C.
证明:∵AB∥CD( ),
∴∠A+∠D=180°( ).
∵AD∥BC( ),
∴________( ).
∴________( ).
请与同伴交流:
(1)∠B和∠D相等吗?
(2)如果一个角的两边与另一个角的两边分别平行,那么这两个角有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线AC‖BD,连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA、PB,构成∠PAC、∠APB、∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是O0)
⑴当动点P落在第①部分时,如图1,求证:∠APB=∠PAC+∠PBD
⑵当动点P落在第②部分时, ∠APB=∠PAC+∠PBD是否成立?在图2中画出图形,若成立,写出推理过程,若不成立,直接写出这三个角之间的关系.
⑶当动点P落在第③部分时,延长BA,点P在射线BA的左侧和右侧时,分别探究∠PAC、∠APB、∠PBD之间 关系,在图3中画出图形,并直接写出相应的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com