
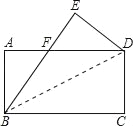
【题目】如图,将矩形ABCD(AB<AD)沿BD折叠后,点C落在点E处,且BE交AD于点F.
(1)若AB=4,BC=8,求DF的长;
(2)当DA平分∠EDB时,求![]() 的值.
的值.
【答案】(1)DF=5;(2)![]() .
.
【解析】
(1)易证BF=FD,在直角△ABF中,根据勾股定理就可以求出DF的长;(2)已知DA平分∠EDB,根据矩形的角是直角,就可以求出∠ADB,∠BDC的度数,就可以把求两线段的比值的问题转化为三角函数的问题.
(1)∵AD∥BC,
∴∠DBC=∠FDB,
又∵∠DBC=∠DBE,
∴∠FDB=∠FBD,
∴BF=FD,
设AF=x,则BF=DF=8﹣x,
在Rt△ABF中,根据勾股定理得到42+x2=(8﹣x)2,
解得x=3,
∴DF=8﹣3=5;
(2)∵DA平分∠EDB,
即∠EDA=∠ADB,
设∠EDA=∠ADB=y°,则∠EDB=2y°,
∴∠BDC=2y°,
∵∠ADC=90°,
∴3y=90°,
解得y=30°,
∴∠DBC=30°,
在Rt△CDB中,tan∠DBC=![]() =tan30°=
=tan30°=![]() ,
,
又∵AB=CD,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】计算题3tan30°﹣|﹣2|+ ![]() +(﹣1)2017;
+(﹣1)2017;
(1)计算:3tan30°﹣|﹣2|+ ![]() +(﹣1)2017;
+(﹣1)2017;
(2)解方程: ![]() =
= ![]() ﹣2.
﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:

![]()
![]()
![]()
⑴ 当黑砖n=1时,白砖有_______块,当黑砖n=2时,白砖有________块,
当黑砖n=3时,白砖有_______块.
⑵ 第n个图案中,白色地砖共 块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论中,正确的有( )①∠1=∠3;②如果∠2=30°则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C

A.①②③B.①②④C.③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)
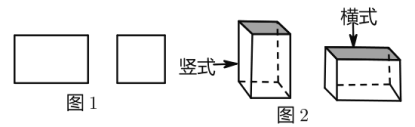
(1)该工厂原计划用若干天加工纸箱200个,后来由于对方急需要货,实际加工时每天加工速度是原计划的1.5倍,这样提前2天超额完成了任务,且总共比原计划多加工40个,问原计划每天加工纸箱多少个?
(2)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办“迎亚运”学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方方形“图中阴影部分”区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽;
(2)如图2,若大长方形的长和宽分别为![]() 和
和![]() .
.
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的![]() ,试求
,试求![]() 的值,
的值,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠CAB=∠DBA,添加下列某条件,未必能判定△ABC≌BAD的是( )
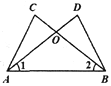
A. AC=BD B. AD=BC C. ∠l=∠2 D. ∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×3.142﹣4×3.14×3.28+3.282”,他觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=﹣1,y=1 | x=1,y=0 | x=3,y=2 | x=1,y=1 | x=5,y=3 | |
A=2x﹣y | ﹣3 | 2 | 4 | 1 | 7 |
B=4x2﹣4xy+y2 | 9 | 4 |
|
|
|
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请结合上述的有关信息,计算4×3.142﹣4×3.14×3.28+3.282.
查看答案和解析>>
科目:初中数学 来源: 题型:
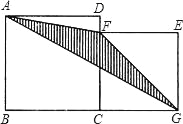
【题目】如图所示,四边形ABCD和CGEF分别是边长为xcm和ycm的正方形,
(1)用含x和y的代数式表示图中阴影部分的面积.
(2)当x=24,y=20时,求此阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com