
 如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )
如图,在矩形ABCD中,AB=4,AD=2,点E、F都对角线AC上,且AE=EF=FC,则线段BE和DF的距离为( )| A. | $\frac{2\sqrt{5}}{3}$ | B. | 1 | C. | $\frac{3\sqrt{17}}{17}$ | D. | $\frac{4\sqrt{17}}{17}$ |
分析 证明△DCF≌△BAE(SAS),得出DF=BE,∠DFC=∠BEA,得出∠DFE=∠BEF,证出DF∥BE,与AE=EF=FC,得出△BCE的面积=$\frac{1}{3}$×8=$\frac{8}{3}$,延长BE交AD于G,延长DF交BC于H,作FM⊥BE于M,CN⊥BE于N,FM∥CN由平行线得出AG=DG=1,BH=CH=1,由勾股定理求出BG=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{17}$,得出BE=$\frac{2}{3}$BG=$\frac{2\sqrt{17}}{3}$,由三角形面积求出CN=$\frac{8\sqrt{17}}{17}$,由三角形中位线定理得出FM=$\frac{1}{2}$CN=$\frac{4\sqrt{17}}{17}$即可.
解答 解:∵矩形ABCD中,AB=4,AD=2,
∴AB∥CD,AB=CD,∠BAD=∠ABC=90°,矩形ABCD的面积=4×2=8,
∴∠DCF=∠BAE,
在△DCF和△BAE中,$\left\{\begin{array}{l}{CD=AB}&{\;}\\{∠DCF=∠BAE}&{\;}\\{CF=AE}&{\;}\end{array}\right.$,
∴△DCF≌△BAE(SAS),
∴DF=BE,∠DFC=∠BEA,
∴∠DFE=∠BEF,
∴DF∥BE,
∵AE=EF=FC,
∴△BCE的面积=$\frac{1}{3}$×8=$\frac{8}{3}$,
延长BE交AD于G,延长DF交BC于H,作FM⊥BE于M,CN⊥BE于N,则FM∥CN,
∵AE=EF=FC,
∴AG=DG=1,BH=CH=1,
∴BG=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{17}$,
∴BE=$\frac{2}{3}$BG=$\frac{2\sqrt{17}}{3}$,
∵$\frac{1}{2}$BE•CN=$\frac{8}{3}$,
∴CN=$\frac{8\sqrt{17}}{17}$,
∵FM∥CN,EF=FC,
∴FM=$\frac{1}{2}$CN=$\frac{4\sqrt{17}}{17}$,
故选:D.
点评 本题考查了矩形的性质、全等三角形的判定与性质、勾股定理、平行线分线段成比例定理等知识;熟练掌握矩形的性质,求出BG是解决问题的关键.


科目:初中数学 来源: 题型:选择题
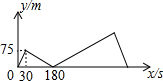 甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )
甲、乙两人在直线道路上同起点,同终点,同方向,分别以不同的速度匀速跑步1500m,先到终点的人原地休息,已知甲先出发30s后,乙才出发,甲、乙两人的距离y(m)与甲出发的时间x(s)之间的关系如图所示,下列说法中错误的是( )| A. | 甲的速度是2.5m/s,乙的速度为3m/s | |
| B. | 乙出发150秒后追上了甲 | |
| C. | 乙到达终点时,甲距终点250m | |
| D. | 甲到达终点比乙晚了70s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )
如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$或$\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
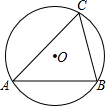 如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )
如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
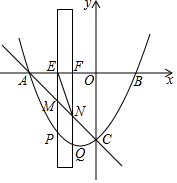 如图,已知抛物线y=$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C,有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
如图,已知抛物线y=$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C,有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com