
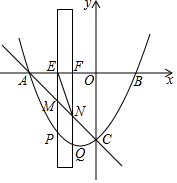
 ��ͼ����֪������y=$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C����һ����Ϊ1�������㹻�ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F��
��ͼ����֪������y=$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C����һ����Ϊ1�������㹻�ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P�͵�Q����ֱ��AC�ڵ�M�͵�N����x���ڵ�E�͵�F������ ��1����y=0�õ�����x�ķ��̿���õ�A�͵�B�ĺ����꣬�ʴ˿���õ�A�͵�B�����꣬��x=0����ö�Ӧ��y��ֵ���ɵõ���C�����ꣻ
��2����EG��AC������Ϊ��G����֤����AEGΪ����ֱ�������Σ��ɵõ�FG�ij���Ȼ�������FN�ij������������ݹ��ɶ��������EN�ij����������������Ǻ����Ķ�����⼴�ɣ�
��3����ֱ��AC�ĺ�������ʽΪy=kx+b������A�͵�C������������k��b��ֵ�ɵõ�AC�Ľ���ʽ����MNΪ��ʱ�����P��n��$\frac{1}{3}$n2+$\frac{2}{3}$n-5�������Q��n+1��$\frac{1}{3}$n2+$\frac{2}{3}$n-6������N��n+1��-n-6����Ȼ�����ݵ�P���N��������֮��Ϊ1�з�����⼴�ɣ���MN��ƽ���ı��εĶԽ���ʱ�����E������Ϊ��m��0������M��m��-m-5����N��m+1��-m-6����P��m��$\frac{1}{3}$m2+$\frac{2}{3}$m-5����Q��m+1��$\frac{1}{3}$��m+1��2+$\frac{2}{3}$��m+1��-5�����������PM=QN�з�����⼴�ɣ�
��� �⣺��1����y=0�ã�$\frac{1}{3}{x}^{2}+\frac{2}{3}$x-5=0�����x=-5��x=3��
�ߵ�B�ڵ�A���Ҳ࣬
���A��B���������-5��0������3��0����
��x=0ʱ��y=-5��
���C��������0��-5����
��2����EG��AC��������G��
�ߵ�E������Ϊ��-4��0����
��OE=4��
��OA=OC=5��
��AE=1����OAC=45�㣮
��AF=FN=2��GE=AE•sin45��=$\frac{\sqrt{2}}{2}$��
��Rt��EFN�У����ݹ��ɶ�����֪NE=$\sqrt{E{F}^{2}+F{N}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
��sin��ANE=$\frac{GE}{EN}$=$\frac{\frac{\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{10}$��
��3����ֱ��AC�ĺ�������ʽΪy=kx+b��
����A�͵�C���������ã�$\left\{\begin{array}{l}{-5k+b=0}\\{b=-5}\end{array}\right.$�����k=-1��b=-5��
��ֱ��AC�ĺ�������ʽΪy=-x-5��
�ٵ�MNΪ��ʱ����ͼ2��ʾ��
���P��n��$\frac{1}{3}$n2+$\frac{2}{3}$n-5�������Q��n+1��$\frac{1}{3}$n2+$\frac{2}{3}$n-6������N��n+1��-n-6����
��$\frac{1}{3}$n2+$\frac{2}{3}$n-6=$\frac{1}{3}$��n+1��2+$\frac{2}{3}$��n+1��-5�����n=-3��
���N��������-2��-3����
��MN��ƽ���ı��εĶԽ���ʱ����ͼ3��ʾ��
���E��������m��0������M��m��-m-5����N��m+1��-m-6����
��PM=QN��P��m��$\frac{1}{3}$m2+$\frac{2}{3}$m-5����Q��m+1��$\frac{1}{3}$��m+1��2+$\frac{2}{3}$��m+1��-5����
��-m-5-��$\frac{1}{3}$m2+$\frac{2}{3}$m-5��=$\frac{1}{3}$��m+1��2+$\frac{2}{3}$��m+1��-5-��-m-6�������m=-3��$\sqrt{6}$��
���N��������-2$+\sqrt{6}$��-3-$\sqrt{6}$����-2-$\sqrt{6}$��-3+$\sqrt{6}$����
�����������Ե�P��Q��N��MΪ������ı�����ƽ���ı���ʱ����N������Ϊ��-2��-3����-2$+\sqrt{6}$��-3-$\sqrt{6}$����-2-$\sqrt{6}$��-3+$\sqrt{6}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˵�������뺯������ʽ�Ĺ�ϵ������ֱ�������ε����ʺ��ж������ɶ�����ƽ���ı��ε����ʣ��ú���ĸn��m��ʽ�ӱ�ʾ����M��P��Q��N�����꣬Ȼ������ƽ�����ı��ε������г�����m��n�ķ����ǽ���Ĺؼ���


 ��ҵ����ϵ�д�
��ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x4+x2=x6 | B�� | ��a+b��2=a2+b2 | C�� | ��3x2y��2=6x4y2 | D�� | ��-m��7�£�-m��2=-m5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AB=4��AD=2����E��F���Խ���AC�ϣ���AE=EF=FC�����߶�BE��DF�ľ���Ϊ��������
��ͼ���ھ���ABCD�У�AB=4��AD=2����E��F���Խ���AC�ϣ���AE=EF=FC�����߶�BE��DF�ľ���Ϊ��������| A�� | $\frac{2\sqrt{5}}{3}$ | B�� | 1 | C�� | $\frac{3\sqrt{17}}{17}$ | D�� | $\frac{4\sqrt{17}}{17}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
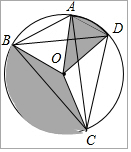 ��֪�ı���ABCD�ǡ�O���ڽӴ�ֱ�ı��Σ�AB=3��CD=4������OA��OB��OC��OD����ͼ������AOD������BOC����ĺͣ�ͼ����Ӱ���֣���
��֪�ı���ABCD�ǡ�O���ڽӴ�ֱ�ı��Σ�AB=3��CD=4������OA��OB��OC��OD����ͼ������AOD������BOC����ĺͣ�ͼ����Ӱ���֣����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
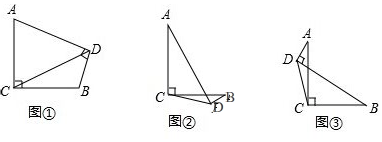
 ��ͼ��DE��AB��E��DF��AC��F����BD=CD��BE=CF��AB=6��AC=10����AE=8��
��ͼ��DE��AB��E��DF��AC��F����BD=CD��BE=CF��AB=6��AC=10����AE=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10�� | B�� | 40���30�� | C�� | 70�� | D�� | 10���70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com