【题目】下列说法不正确的是（ ）
A. 了解全市中学生对泰州“三个名城”含义的知晓度的情况，适合用抽样调查
B. 若甲组数据方差S甲2=0.39，乙组数据方差S乙2=0.27，则乙组数据比甲组数据稳定
C. 某种彩票中奖的概率是
，买100张该种彩票一定会中奖
D. 数据﹣1、1.5、2、2、4的中位数是2
阅读快车系列答案科目：初中数学 来源： 题型：
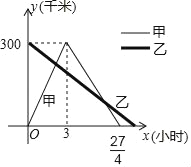
【题目】已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是甲乙两车离A地的距离y（千米）与行驶时间x（小时）之间的函数图象．
（1）求甲车离A地的距离y甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
（2）若它们出发第5小时时，离各自出发地的距离相等，求乙车离A地的距离y乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
（3）在（2）的条件下，求它们在行驶的过程中相遇的时间．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地长途汽车站规定前来乘车的旅客可以免费随身携带一定质量的行李，如果行李质量超过规定，则应交纳行李费，行李费用y（元）与行李质量x（千克）之间的关系可以用如图所示的图象表示，请观察图象回答下列问题：
（1）旅客最多能免费携带多少千克的行李？
（2）求行李费用y（元）与行李质量x（千克）之间的函数关系式；
（3）一位旅客随身携带了60千克的行李，他应交纳行李费多少元？
（4）另一位旅客交纳了120元行李费，他携带的行李重多少千克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形ABC（顶点是网格线的交点的三角形）的顶点B、C的坐标分别为（﹣2，0），（﹣1，2）．
（1）请在如图所示的网格中根据上述点的坐标建立对应的直角坐标系；（只要画图，不需要说明）
（2）在（1）中建立的平面直角坐标系中，先画出△ABC关于y轴对称的图形△A1B1C1，再画出△A1B1C1关于x轴对称的图形△A2B2C2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，大刚在晚上由灯柱A走向灯柱B，当他走到M点时，发觉他身后影子的顶部刚好接触到灯柱A的底部，当他向前再走12米到N点时，发觉他身前的影子刚好接触到灯柱B的底部，已知大刚的身高是1.6米，两根灯柱的高度都是9.6米，设AM=NB=x米．求：两根灯柱之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,用直尺和圆规作一个角∠A′O′B′,等于已知角∠AOB,能得出∠A′O′B′=∠AOB的依据是( )
A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中, ∠ACB=90,AC=BC, 直线MN经过点C,且AD⊥MN,BE⊥MN,垂足分别为D,E.
(1) 若直线MN在图①位置时,猜想AD,BE,DE三条线段具有怎样的数量关系?并且给出证明.
(2) 当直线MN在图②位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,给出新的结论,并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（0，2），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3
，则点B′的坐标为（ ）
A. （2，4） B. （2，3） C. （3，4） D. （3，3）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道“两边和一角分别相等的两个三角形不一定全等”，如图（1），
，
，
，但
与
却不全等.但是如果两个直角三角形呢？如图（2）
，
，
,则
吗？
（1）根据图（2）完成以下证明和阅读：
和
中，
，
____________（勾股定理）
，
____________
，.
____________
在与中，
，，
____________（____________）
归纳：斜边和一条直角边相等的两个直角三角形全等；简称为“斜边直角边”或“
”.
几何语言如下：
在与中，
，
（2）如图（3）已知
，
；求证：
平分
.（每一步都要填写理由）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
