
(2)方法有:_______法或_______法.
| (1)整式 提示:  
练习册系列答案
相关习题
科目:初中数学 来源: 题型:阅读理解 (2012•湛江)先阅读理解下面的例题,再按要求解答下列问题: 例题:解一元二次不等式x2-4>0 解:∵x2-4=(x+2)(x-2) ∴x2-4>0可化为 (x+2)(x-2)>0 由有理数的乘法法则“两数相乘,同号得正”,得 ①
解不等式组①,得x>2, 解不等式组②,得x<-2, ∴(x+2)(x-2)>0的解集为x>2或x<-2, 即一元二次不等式x2-4>0的解集为x>2或x<-2. (1)一元二次不等式x2-16>0的解集为 x>4或x<-4 x>4或x<-4 ;(2)分式不等式
x>3或x<1 x>3或x<1 ;(3)解一元二次不等式2x2-3x<0. 查看答案和解析>> 科目:初中数学 来源:2012年初中毕业升学考试(广东湛江卷)数学(带解析) 题型:解答题 先阅读理解下面的例题,再按要求解答下列问题: 查看答案和解析>> 科目:初中数学 来源:2012年初中毕业升学考试(广东湛江卷)数学(解析版) 题型:解答题 先阅读理解下面的例题,再按要求解答下列问题: 例题:解一元二次不等式x2﹣4>0 解:∵x2﹣4=(x+2)(x﹣2) ∴x2﹣4>0可化为 (x+2)(x﹣2)>0 由有理数的乘法法则“两数相乘,同号得正”,得
解不等式组①,得x>2, 解不等式组②,得x<﹣2, ∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2, 即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2. (1)一元二次不等式x2﹣16>0的解集为 ; (2)分式不等式 (3)解一元二次不等式2x2﹣3x<0.
查看答案和解析>> 科目:初中数学 来源:广东省中考真题 题型:解答题 先阅读理解下面的例题,再按要求解答下列问题: 例题:解一元二次不等式x2﹣4>0 解:∵x2﹣4=(x+2)(x﹣2) ∴x2﹣4>0可化为 (x+2)(x﹣2)>0 由有理数的乘法法则“两数相乘,同号得正”, 得 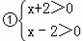 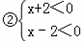 解不等式组①,得x>2,解不等式组②,得x<﹣2, ∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2, 即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2. (1)一元二次不等式x2﹣16>0的解集为 ; (2)分式不等式 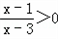 的解集为 ; 的解集为 ;(3)解一元二次不等式2x2﹣3x<0. 查看答案和解析>> 科目:初中数学 来源:2013年广东省中考数学模拟试卷(二十)(解析版) 题型:解答题 先阅读理解下面的例题,再按要求解答下列问题: 例题:解一元二次不等式x2-4>0 解:∵x2-4=(x+2)(x-2) ∴x2-4>0可化为 (x+2)(x-2)>0 由有理数的乘法法则“两数相乘,同号得正”,得 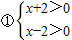 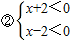 解不等式组①,得x>2, 解不等式组②,得x<-2, ∴(x+2)(x-2)>0的解集为x>2或x<-2, 即一元二次不等式x2-4>0的解集为x>2或x<-2. (1)一元二次不等式x2-16>0的解集为______; (2)分式不等式 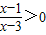 的解集为______; 的解集为______;(3)解一元二次不等式2x2-3x<0. 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |