
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |

| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| OD |
| OP |
| OC |
| O′C |
| OD |
| OP |
| OC |
| O′C |
| 8 |
| 12 |
| 6 |
| O′C |
| 39 |
| 4 |
| 39 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 39 |
| 4 |
| 3 |
| 2 |
| 39 |
| 4 |


科目:初中数学 来源: 题型:
 某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元.
某衬衫厂,生产某品牌衬衫的成本价位50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍,批发价不低于55元.查看答案和解析>>
科目:初中数学 来源: 题型:
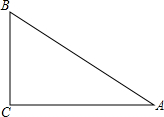
 如图,在5×5的正方形网格中,每个小正方形的边长都为1,线段AB的端点都落在格点(即小正方形的顶点)上.请以AB为一边画一个等腰三角形ABC,使点C在格点上,并求所画三角形ABC的面积.
如图,在5×5的正方形网格中,每个小正方形的边长都为1,线段AB的端点都落在格点(即小正方形的顶点)上.请以AB为一边画一个等腰三角形ABC,使点C在格点上,并求所画三角形ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
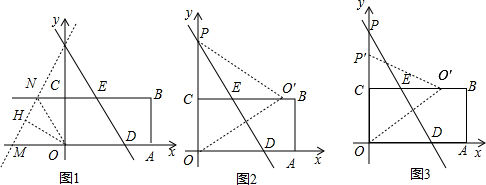
 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com