

 ;
; (2分);当x>100时,
(2分);当x>100时,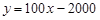 。
。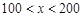 时,选择方案二总费用最省;
时,选择方案二总费用最省;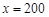 时,方案一、二均可;当
时,方案一、二均可;当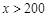 时,选择方案一,总费用最省。
时,选择方案一,总费用最省。

 53天天练系列答案
53天天练系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 台,所有型号空调全部售出后获得的总利润为
台,所有型号空调全部售出后获得的总利润为 元.
元. 与
与 之间的函数关系式.
之间的函数关系式. 元(
元( ),其余型号售价不变,则商场又该如何采购才能获得最大利润?
),其余型号售价不变,则商场又该如何采购才能获得最大利润?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com