
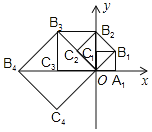
【题目】如图,在平面直角坐标系中,边长为1的正方形![]() 的两边在坐标轴上,以它的对角线
的两边在坐标轴上,以它的对角线![]() 为边作正方形
为边作正方形![]() ,再以正方形
,再以正方形![]() 的对角线
的对角线![]() 为边作正方形
为边作正方形![]() ,以此类推
,以此类推![]() 、则正方形
、则正方形![]() 的顶点
的顶点![]() 的坐标是______.
的坐标是______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() ,点
,点![]() 和点
和点![]() 是
是![]() 上关于直线
上关于直线![]() 对称的两个点,连接
对称的两个点,连接![]() 、
、![]() ,且
,且![]() ,直线
,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作直线
作直线![]() 与线段
与线段![]() 的延长线相交于点
的延长线相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,且
,且![]() .
.

(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)若点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,满足
,满足![]() ,
,
①求证:![]() ;
;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
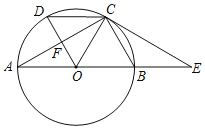
【题目】AB是⊙O的直径,C点在⊙O上,F是AC的中点,OF的延长线交⊙O于点D,点E在AB的延长线上,∠A=∠BCE.
(1)求证:CE是⊙O的切线;
(2)若BC=BE,判定四边形OBCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
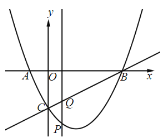
【题目】如图,在平面直角坐标系中,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴下方的抛物线上一动点(包含点
轴下方的抛物线上一动点(包含点![]() ,
,![]() ).作直线
).作直线![]() ,若过点
,若过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)在点![]() 运动的过程中,请求出
运动的过程中,请求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,使
,使![]() 是等腰三角形.若存在,请直接写出点
是等腰三角形.若存在,请直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是![]() ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
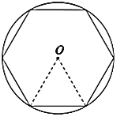
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率![]() 的近似值.如图,设半径为
的近似值.如图,设半径为![]() 的圆内接正
的圆内接正![]() 边形的周长为
边形的周长为![]() ,圆的直径为
,圆的直径为![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ______.(结果精确到0.01,参考数据:
______.(结果精确到0.01,参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.
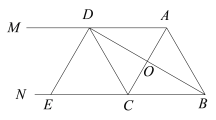
(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一不透明的袋子中装有四张标有数字![]() 的卡片,这些卡片除数字外其余均相同.小明同学按照一定的规则抽出两张卡片,并把卡片上的数字相加,下图是他所画的树状图的一部分.
的卡片,这些卡片除数字外其余均相同.小明同学按照一定的规则抽出两张卡片,并把卡片上的数字相加,下图是他所画的树状图的一部分.
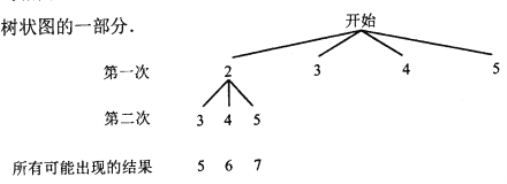
(1)由上图分析,该游戏规则是:第一次从袋子中随机抽出一张卡片后 (填“放回”或“不放回”),第二次随机再抽出一张卡片;
(2)帮小明同学补全树状图,并求小明同学两次抽到卡片上的数字之和为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com