
如图,在ΔABC中,∠ABC=90,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF
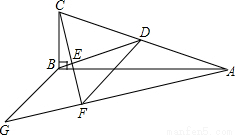
(1)猜想四边形BDFG的形状,并说明理由
(2)若AF=8,CF=6,求四边形BDFG的周长
(1)四边形BDFG是菱形(2)周长为20
【解析】
试题分析:(1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形;
(2)首先过点B作BH⊥AG于点H,由AF=8,CF=6,可利用勾股定理求得AC的长,即可求得DF的长,然后由菱形的性质求得BG=GF=DF=5,又由∠G=30°,即可求得BH的长,继而求得四边形BDFG的面积.
试题解析::(1)四边形BDFG是菱形.
理由:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CE⊥BD,
∴CE⊥AG,
又∵BD为AC的中线,
∴BD=DF=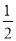 AC,
AC,
∴四边形BDFG是菱形,
(2)过点B作BH⊥AG于点H,
∵AF=8,CF=6,CF⊥AG,
∴AC=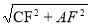 =10,
=10,
∴DF=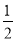 AC=5,
AC=5,
∵四边形BDFG是菱形,
∴BD=GF=DF=5,
∴C菱形BDFG=4BD=20.

考点:1.菱形的判定与性质;2.直角三角形斜边上的中线.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题满分12分)在平面直角坐标系中,抛物线C :y=
:y= x
x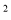 +4x+4
+4x+4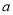 (0<
(0<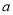 <2),
<2),


(1)当C 与x轴有唯一交点时,求C
与x轴有唯一交点时,求C 的解析式;
的解析式;
(2)若 =1,将抛物线C
=1,将抛物线C 先向右平移2个单位,再向下平移1个单位得抛物线C
先向右平移2个单位,再向下平移1个单位得抛物线C ,抛物线C
,抛物线C 与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C
与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C 相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
(3)若A(1,y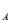 ),B(0,y
),B(0,y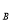 ),C(-1,y
),C(-1,y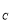 )三点均在C
)三点均在C 上,连BC,作AE∥BC交抛物线C
上,连BC,作AE∥BC交抛物线C 于E,求证:当
于E,求证:当 值变化时,E点在一条直线上.
值变化时,E点在一条直线上.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市七年级下学期第一次月考数学试卷(解析版) 题型:选择题
PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
A、0.25×10-5 B、0.25×10-6
C、2.5×10-5 D、2.5×10-6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(6分)如图,在一块长35m,宽26m的矩形地面上,修建同样宽的两条互相垂直的道路(两条道路与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m,道路的宽应为多少?

查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
如图,把一个长方形的纸片沿EF折叠后, 点D、C分别落在点M、N的位置, 如果∠EFB=65,那么∠AEM等于 .
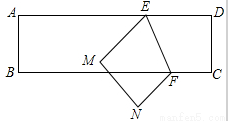
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市高港实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分)如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.

(1)格点△ABC的面积为 ;
(2)画出格点△ABC绕点C逆时针旋转90°后的△A1B1C1,并求出在旋转过程中,点B所经过的路径长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期第一次质检数学试卷(解析版) 题型:选择题
设a为最小的正整数,b为最大的负整数,c是绝对值最小的有理数,则a-b+c的值为( )
A.2 B.-2 C.2或-2 D.以上都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com