
(本题满分12分)在平面直角坐标系中,抛物线C :y=
:y= x
x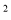 +4x+4
+4x+4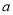 (0<
(0<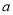 <2),
<2),


(1)当C 与x轴有唯一交点时,求C
与x轴有唯一交点时,求C 的解析式;
的解析式;
(2)若 =1,将抛物线C
=1,将抛物线C 先向右平移2个单位,再向下平移1个单位得抛物线C
先向右平移2个单位,再向下平移1个单位得抛物线C ,抛物线C
,抛物线C 与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C
与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C 相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
(3)若A(1,y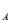 ),B(0,y
),B(0,y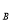 ),C(-1,y
),C(-1,y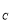 )三点均在C
)三点均在C 上,连BC,作AE∥BC交抛物线C
上,连BC,作AE∥BC交抛物线C 于E,求证:当
于E,求证:当 值变化时,E点在一条直线上.
值变化时,E点在一条直线上.
(1)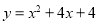 ;(2)
;(2)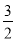 ;(3)证明详见解析.
;(3)证明详见解析.
【解析】
试题分析:(1)根据二次函数与一元二次方程的关系,可知 有两个相等的实数根,据此求出a的值;
有两个相等的实数根,据此求出a的值;
(2)设P( ,
, ),Q(
),Q( ,
,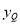 ),得到
),得到 、
、 为方程
为方程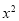 -1=kx的两根,∴
-1=kx的两根,∴
 =-1 ∴
=-1 ∴ =-
=- ,
, =2,进而得到k=
=2,进而得到k=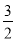 ;
;
(3)作CD⊥y轴于D,作AQ⊥x轴于Q,作EG⊥AQ于G,则△AEG∽△BCD,设E(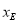 ,
,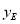 ) ,得到关于
) ,得到关于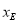 的等式,解得
的等式,解得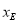 的值,即可得到点E所在的直线关系式.
的值,即可得到点E所在的直线关系式.
试题解析:(1)抛物线C 与x轴有唯一交点,即当y=0时,
与x轴有唯一交点,即当y=0时, 有两个相等的实数根,此时
有两个相等的实数根,此时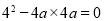 ,解得:a=
,解得:a= ,因为0<
,因为0< <2,所以a=1,所以抛物线C
<2,所以a=1,所以抛物线C 的解析式为
的解析式为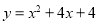 ;
;
(2)设P( ,
, ),Q(
),Q( ,
,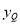 ),则:
),则: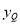 =-4
=-4 ,∴
,∴ =-4
=-4 ,且
,且 、
、 为方程
为方程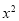 -1=kx的两根,∴
-1=kx的两根,∴
 =-1 ∴
=-1 ∴ =-
=- ,
, =2,∴k=
=2,∴k=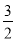 .
.
(3) 作CD⊥y轴于D,作AQ⊥x轴于Q,作EG⊥AQ于G,则△AEG∽△BCD,∴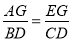 ,设E(
,设E(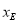 ,
,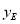 ) ,∴
) ,∴ =a+4+4a ,
=a+4+4a , =4a ,
=4a ,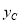 =a-4+4a,
=a-4+4a,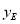 =a
=a +4
+4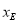 +4a,∴
+4a,∴ ,∵
,∵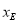 ≠1,∴
≠1,∴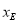 =-2,即E点在直线x=-2上.
=-2,即E点在直线x=-2上.

考点:二次函数与一元二次方程的关系;二次函数的综合应用.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
下列四个点中,在反比例函数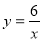 的图像上的是( )
的图像上的是( )
A.(1,-6) B.(2,4) C.(3,-2) D.(-6,-1)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:选择题
一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若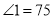 ,则
,则 的大小是( ).
的大小是( ).
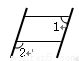
A.75 B.115 C.65 D.105
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题满分8分)为响应我市“中国梦”“武汉梦”主题教育活动,某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
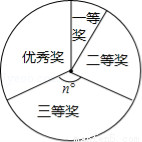

请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ,n= .
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题8分)如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
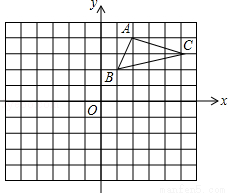
(1)画出△ABC关于x轴对称的△A1B1C1,并直接写出点A1的坐标.(4分)
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,若△A1B1C1内一点P的坐标为(a,b),请直接写出点P在△A2B2C2内对应点P′的坐标.(4分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,在ΔABC中,∠ABC=90,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF
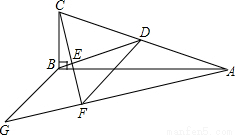
(1)猜想四边形BDFG的形状,并说明理由
(2)若AF=8,CF=6,求四边形BDFG的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com