
按如图所示的方法折纸,下面结论正确的个数( )
①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.


A.1个 B.2个 C.3个 D.4个
C
【考点】翻折变换(折叠问题);相似三角形的判定与性质.
【分析】根据翻折变换的性质、相似三角形的判定定理解答即可.
【解答】解:由翻折变换的性质可知,∠AEB+∠FEC=
 ×180°=90°,
×180°=90°,
则∠AEF=90°,即∠2=90°,①正确;
由图形可知,∠1<∠AEC,②错误;
∵∠2=90°,
∴∠1+∠3=90°,又∠1+∠BAE=90°,
∴∠BAE=∠3,④正确;
∵∠BAE=∠3,∠B=∠C=90°,
∴△ABE∽△ECF,③正确.
故选:C.
【点评】本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
在一个不透明的袋中装有3 个完全相同的小球,上面分别标号为1、2、3,从中随机摸出两个小球,并用球上的数字组成一个两位数.
(1)求组成的两位数是奇数的概率;
(2)小明和小华做游戏,规则是:若组成的两位数是4的倍数,小明得3分,否则小华得3分,你认为该游戏公平吗?说明理由;若不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第三组(79.5~89.5)”的扇形的圆心角为 度;
(2)若成绩在90分以上(含90分)的同学可以获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3,则下列判断中正确的是( )


A.此抛物线的解析式为y=x2+x﹣2
B.当x>0时,y随着x的增大而增大
C.在此抛物线上的某点M,使△MAB的面积等于5,这样的点共有三个
D.此抛物线与直线y=﹣
 只有一个交点
只有一个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
C.“明天降雨的概率为
 ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
已知在直角坐标系中,抛物线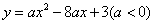 与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
(1)当AB=BD时(如图),求抛物线的表达式;
(2)在第(1)小题的条件下,当DP∥AB时,求点P的坐标;
(3)点G在对称轴BD上,且 ,求△ABG的面积.
,求△ABG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时
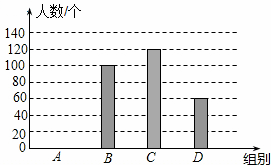
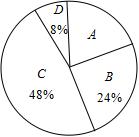
根据以上信息,回答下列问题:
(1) A组的人数是__________人,并不全条形统计图
(2) 本次调查数据的中位数落在组__________
(3) 根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有__________人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com