
��ͼ����ƽ��ֱ������ϵ�У�������y=x2+bx+c��x�ύ��A��B���㣬��A��x��ĸ����ᣬ��B��x��������ᣬ��y�ύ�ڵ�C����CO=2AO��CO=BO��AB=3���������ж�����ȷ���ǣ�������


A���������ߵĽ���ʽΪy=x2+x��2
B����x��0ʱ��y����x�����������
C���ڴ��������ϵ�ij��M��ʹ��MAB���������5�������ĵ㹲������
D������������ֱ��y=��
 ֻ��һ������
ֻ��һ������
��
D�����㡿��������x��Ľ��㣮
����������ȷ��A��B������꣬������ý���ʽ��������߽���ʽ�����ǿɶ�Aѡ������жϣ����ݶ��κ��������ʶ�Bѡ������жϣ���M��t��t2��t��2�������������������ʽ�õ�
 ��3��|t2��t��2|=5���ٰѷ��̻�Ϊt2��t��2=
��3��|t2��t��2|=5���ٰѷ��̻�Ϊt2��t��2=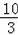
 ��t2��t��2=��
��t2��t��2=��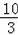
 ��Ȼ��ͨ������������ȷ��t��ֵ���Ӷ��ɶ�Cѡ������жϣ�ͨ���ⷽ��x2��x��2=��
��Ȼ��ͨ������������ȷ��t��ֵ���Ӷ��ɶ�Cѡ������жϣ�ͨ���ⷽ��x2��x��2=��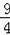
 �ɶ�Dѡ������жϣ�
�ɶ�Dѡ������жϣ�
����𡿽⣺��CO=2AO��CO=BO��AB=3��
��OA=1��OB=2��
��A����1.0����B��2��0����
�������߽���ʽΪy=��x+1����x��2������y=x2��x��2������Aѡ�����
�������ߵĶԳ���Ϊֱ��x=
 ��
��
�൱x��
 ʱ��y����x���������������Bѡ�����
ʱ��y����x���������������Bѡ�����
��M��t��t2��t��2����
����MAB���������5����
 ��3��|t2��t��2|=5��
��3��|t2��t��2|=5��
��t2��t��2=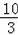
 ��t2��t��2=��
��t2��t��2=��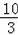
 ��
��
�߷���t2��t��2=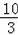
 ����������ʵ���⣬�����̻�t2��t��2=��
����������ʵ���⣬�����̻�t2��t��2=��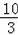
 û��ʵ���⣬
û��ʵ���⣬
������������M����2��������Cѡ�����
��y=��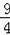
 ʱ��x2��x��2=��
ʱ��x2��x��2=��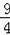
 �����x1=x2=
�����x1=x2=

����������ֱ��y=��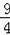
 ֻ��һ�����㣬����Dѡ����ȷ��
ֻ��һ�����㣬����Dѡ����ȷ��
��ѡD��
�����������⿼������������x��Ľ��㣺������κ���y=ax2+bx+c��a��b��c�dz�����a��0����x��Ľ�������ת��Ϊ�����x��һԪ���η��̣�Ҳ�����˸����б�ʽ����ϵ���Ĺ�ϵ�����ڶ��κ���y=ax2+bx+c��a��b��c�dz�����a��0������=b2��4ac������������x��Ľ����������=b2��4ac��0ʱ����������x����2�����㣻��=b2��4ac=0ʱ����������x����1�����㣻��=b2��4ac��0ʱ����������x��û�н��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ʦ�ںڰ���д��һ����ȷ��������̣������������ס�˵Ķ���ʽ����ʽ���£�

 ����a+2b��2=a2��4b2
����a+2b��2=a2��4b2
��1��������Ķ���ʽ��
��2����a=��1��b=
 ʱ������Ķ���ʽ��ֵ��
ʱ������Ķ���ʽ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ͼ��ʾ�ķ�����ֽ�����������ȷ�ĸ�����������
�١�2=90�㣻�ڡ�1=��AEC���ۡ�ABE�ס�ECF���ܡ�BAE=��3��


A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�����ĸ���С��ͬ����������ɵļ����壬��ô��������ͼ�ǣ�������


A��
 B��
B��
 C��
C��
 D��
D��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�ڷֱ�д������-1,0,2,3�����ſ�Ƭ�������ȡһ�ţ��Żغ��ٳ�ȡһ�ţ�����Ե�һ�γ�ȡ��������Ϊ�����꣬�ڶ��γ�ȡ��������Ϊ�����꣬��ô���õ����ڵ�һ���ĸ���Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ1����ƽ��ֱ������ϵxOy�У�������M�� ������C(2��3)��ֱ��y��kx��b���������ཻ��A��B���㣬��ACB��90��
������C(2��3)��ֱ��y��kx��b���������ཻ��A��B���㣬��ACB��90��
(1) ̽�������
�� ̽����
ȡ��B(6��﹣13)ʱ����A������Ϊ( ��
�� )��ֱ��д��ֱ��AB�Ľ���ʽ ��ȡ��B(4��﹣3)��ֱ��д��AB�Ľ���ʽΪ
)��ֱ��д��ֱ��AB�Ľ���ʽ ��ȡ��B(4��﹣3)��ֱ��д��AB�Ľ���ʽΪ
�� ���룺
���Dz���ֱ��AB�ؾ���һ������Q��������Ϊ ����ȡ��B�ĺ�����Ϊn����֤��IJ��룻
�������ѣ��������û�н������Ӱ���(2)�ʵĽ��
(2) ��ͼ2����D��������M�ϣ���AB����ԭ��O����ABD��������ڡ�ABC������������һ�����������ĵ�D�����꣬��ֱ��д������ķ���������D�������


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com