按一定规律排列的一列数依次为：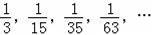
，按此规律排列下去，这列数中的第7个数是
．
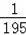
【考点】规律型：数字的变化类．
【分析】首先根据题意，可得每个数的分子都是1；然后根据第一个数的分母3=1×3=（2×1﹣1）×（2×1+1），第二个数的分母15=3×5=（2×2﹣1）×（2×2+1），第三个数的分母35=5×7=（2×3﹣1）×（2×3+1），第四个数的分母63=7×9=（2×4﹣1）×（2×4+1），…，可得第n个数的分母是2n﹣1与2n+1的乘积，据此求出这列数中的第7个数的分母是多少，进而求出它的值是多少即可．
【解答】解：每个分数的分子都是1，
因为3=1×3=（2×1﹣1）×（2×1+1），
15=3×5=（2×2﹣1）×（2×2+1），
35=5×7=（2×3﹣1）×（2×3+1），
63=7×9=（2×4﹣1）×（2×4+1），
…，
所以第n个数的分母是2n﹣1与2n+1的乘积，
所以这列数中的第7个数是：
．
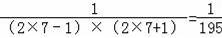
故答案为：．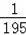
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
下列说法中，正确的是( )
A.sin600+cos300=1.
B.若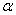
为锐角，则
﹦1﹣sin.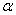
C.对于锐角
，必有
.
D.在Rt△ABC中,∠C=90
，则有
.
查看答案和解析>>
科目：初中数学 来源： 题型：
在一个不透明的袋中装有3 个完全相同的小球，上面分别标号为1、2、3，从中随机摸出两个小球，并用球上的数字组成一个两位数．
（1）求组成的两位数是奇数的概率；
（2）小明和小华做游戏，规则是：若组成的两位数是4的倍数，小明得3分，否则小华得3分，你认为该游戏公平吗？说明理由；若不公平，请修改游戏规则，使游戏公平．
查看答案和解析>>
科目：初中数学 来源： 题型：
为增强学生环保意识，某中学组织全校2000名学生参加环保知识大赛，比赛成绩均为整数，从中抽取部分同学的成绩进行统计，并绘制成如图统计图．请根据图中提供的信息，解答下列问题：
（1）若抽取的成绩用扇形图来描述，则表示“第三组（79.5～89.5）”的扇形的圆心角为 度；
（2）若成绩在90分以上（含90分）的同学可以获奖，请估计该校约有多少名同学获奖？
（3）某班准备从成绩最好的4名同学（男、女各2名）中随机选取2名同学去社区进行环保宣传，则选出的同学恰好是1男1女的概率为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点，点A在x轴的负半轴，点B在x轴的正半轴，与y轴交于点C，且CO=2AO，CO=BO，AB=3，则下列判断中正确的是（ ）
A．此抛物线的解析式为y=x2+x﹣2
B．当x＞0时，y随着x的增大而增大
C．在此抛物线上的某点M，使△MAB的面积等于5，这样的点共有三个
D．此抛物线与直线y=﹣
只有一个交点
查看答案和解析>>
科目：初中数学 来源： 题型：
已知在直角坐标系中，抛物线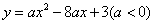
与y轴交于点A，顶点为D，其对称轴交x轴于点B，点P在抛物线上，且位于抛物线对称轴的右侧.
(1)当AB=BD时（如图），求抛物线的表达式；
(2)在第(1)小题的条件下，当DP∥AB时，求点P的坐标；
(3)点G在对称轴BD上，且
，求△ABG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，BC=8，则AC等于（ ）
C．10 D．12
B．
D．
，则
的值是 。