练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知圆锥的底面半径为4cm，高为3cm，则圆锥的侧面积是（　　）
    A．20cm2B．20πcm2C．12πcm2D．10πcm2

    分析 根据圆锥的底面半径和高求出圆锥的母线长，再根据圆锥的底面周长等于圆锥的侧面展开扇形的弧长，最后利用扇形的面积计算方法求得侧面积．

    解答 解：由勾股定理得：圆锥的母线长=$\sqrt{{3}^{2}+{4}^{2}}$=5，
    ∵圆锥的底面周长为2πr=2π×4=8π，
    ∴圆锥的侧面展开扇形的弧长为8π，
    ∴圆锥的侧面积为：$\frac{1}{2}$×8π×5=20π．
    故选B．

    点评 本题考查了圆锥的侧面积的计算方法，解决本题的关键是根据已知条件求出圆锥的母线长和侧面展开扇形的弧长，然后用弧长与母线长乘积的一半求扇形的面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．在下列各电视台的台标图案中，是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

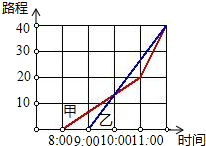    13．如图，它表示甲乙两人从同一个地点出发后的情况．到十点时，甲大约走了13千米．根据图象回答：
    （1）甲是几点钟出发？
    （2）乙是几点钟出发，到十点时，他大约走了多少千米？
    （3）到十点为止，哪个人的速度快？
    （4）两人最终在几点钟相遇？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

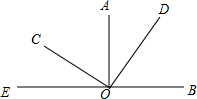    10．如图，已知AO⊥BE于O点，CO⊥DO于O点，∠BOC=α，则∠AOD的度数为（　　）
    A．α-90°B．2α-90°C．180°-αD．2α-180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）$\sqrt{5}$+2$\sqrt{5}$-5$\sqrt{5}$            
    （2）$\root{3}{-8}$×$\sqrt{2\frac{1}{4}}$÷$\root{3}{（\frac{1}{8}）^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．在△ABC中，∠ABC=30°，∠BAC=70°．在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画（　　）
    A．7条B．8条C．9条D．10条

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算或化简：
    （1）$\frac{2}{{\sqrt{2}}}$+（-$\sqrt{2}$+1）0-2sin45°               
    （2）$\frac{{{x^2}-1}}{{{x^2}+x}}÷（{x-\frac{2x-1}{x}}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，在?ABCD中，对角线AC，BD交于点E，AC⊥BC，若BC=5，AB=13，则BD的长是2$\sqrt{61}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，已知AD∥BC，∠1=∠2，∠3=∠4，点E在DC上，求证：AD+BC=AB．

    查看答案和解析>>

    同步练习册答案