
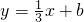 与新图象只有一个公共点P(x0,y0)且 y0≤7时,求b的取值范围.
与新图象只有一个公共点P(x0,y0)且 y0≤7时,求b的取值范围.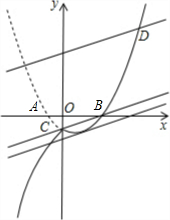 解:(1)∵抛物线y=(m-1)x2+(m-2)x-1与x轴交于A、B两点,
解:(1)∵抛物线y=(m-1)x2+(m-2)x-1与x轴交于A、B两点,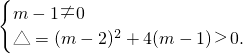
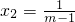 .
.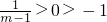 .
.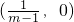 .
. .
.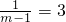 .
. .
. .
.  与y轴的交点,
与y轴的交点,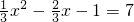 .
.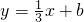 经过D点时,可得b=5.
经过D点时,可得b=5.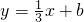 经过C点时,可得b=-1.
经过C点时,可得b=-1.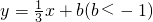 与函数
与函数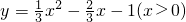
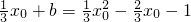 .
. .
.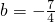 .
. .
.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为| 15 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-| 1 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com