
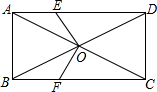
 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF. 证明:如图,∵四边形ABCD是矩形,
证明:如图,∵四边形ABCD是矩形,| 1 |
| 2 |
| 1 |
| 2 |
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
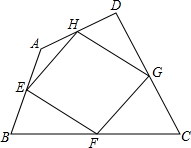 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):| 数据段 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 总计 |
| 频 数 | 10 | 40 | 20 | |||
| 百分比 | 5% | 40% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com