
 x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.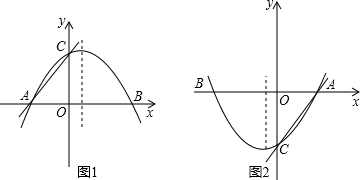 解:根据OC长为8可得一次函数中的n的值为8或-8.
解:根据OC长为8可得一次函数中的n的值为8或-8.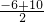 =2,
=2,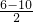 =-2,
=-2,

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
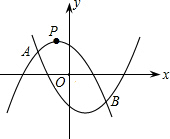
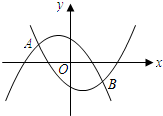 ,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?查看答案和解析>>
科目:初中数学 来源: 题型:044
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设A(x1,y1)、B(x2,y2)是抛物线与直线的两个交点,点P是线段AB的中点,且点P的横坐标为![]() ,试用含a的代数式表示点P的纵坐标;
,试用含a的代数式表示点P的纵坐标;
(3)设A,B两点的距离d=![]() ·|x1-x2|,试用含a的代数式表示d.
·|x1-x2|,试用含a的代数式表示d.
查看答案和解析>>
科目:初中数学 来源:2008年江西省中考数学试卷(解析版) 题型:解答题
 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com