练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施，为了了解居民对慈善法的知晓情况，某街道办从辖区居民中随机选取了部分居民进行调查，并将调查结果绘制成如图所示的扇形图．若该辖区约有居民9000人，则可以估计其中对慈善法“非常清楚”的居民约有人．

    【答案】2700
    【解析】解：根据题意得：9000×（1﹣30%﹣15%﹣ ×100%）
    =9000×30%
    =2700（人）．
    答：可以估计其中对慈善法“非常清楚”的居民约有2700人．
    故答案为：2700．
    先求出非常清楚所占的百分百，再乘以该辖区的总居民，即可得出答案．此题考查了用样本估计总体，在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．

    （一）尝试探究
    如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD上，∠EAF=30°，连接EF．
    （1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=度，线段BE、EF、FD之间的数量关系为 ．
    （2）如图3，当点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=ax2﹣6x+c与x轴交于点A（﹣5，0）、B（﹣1，0），与y轴交于点C（0，﹣5），点P是抛物线上的动点，连接PA、PC，PC与x轴交于点D．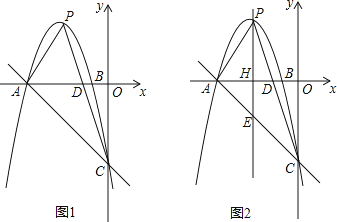

    （1）求该抛物线所对应的函数解析式；
    （2）若点P的坐标为（﹣2，3），请求出此时△APC的面积；
    （3）过点P作y轴的平行线交x轴于点H，交直线AC于点E，如图2．
    ①若∠APE=∠CPE，求证： ；
    ②△APE能否为等腰三角形？若能，请求出此时点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知A（a，0），B （0，b）分别为两坐标轴上的点，且a，b满足a2﹣24a+|b﹣12|=﹣144，且3OC=OA．

    （1）求A、B、C三点的坐标；

    （2）若D（2，0），过点D的直线分别交AB、BC于E、F两点，且DF=DE，设E、F两点的横坐标分别为xE、xP，求xE+xP的值；

    （3）如图2，若M（4，8），点P是x轴上A点右侧一动点，AH⊥PM于点H，在HM上取点G，使HG=HA，连接CG，当点P在点A右侧运动时，∠CGM的度数是否改变？若不变，请求其值；若改变，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了解全校同学五一假期参加社团活动的情况，抽查了100名同学，统计它们假期参加社团活动的时间，绘成频数分布直方图（如图），则参加社团活动时间的中位数所在的范围是（　　）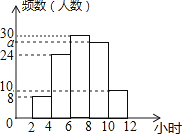

    A.4﹣6小时
    B.6﹣8小时
    C.8﹣10小时
    D.不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】深圳市政府计划投资1.4万亿元实施东进战略．为了解深圳市民对东进战略的关注情况．某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下：

    关注情况

    频数

    频率

    A．高度关注

    M

    0.1

    B．一般关注

    100

    0.5

    C．不关注

    30

    N

    D．不知道

    50

    0.25


    （1）根据上述统计图可得此次采访的人数为人，m= ， n=
    （2）根据以上信息补全条形统计图；
    （3）根据上述采访结果，请估计在15000名深圳市民中，高度关注东进战略的深圳市民约有人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】表为甲班55人某次数学小考成绩的统计结果，关于甲班男、女生此次小考成绩的统计量，下列叙述何者正确？（　　）

    成绩（分）

    50

    70

    90

    男生（人）

    10

    10

    10

    女生（人）

    5

    15

    5

    合计（人）

    15

    25

    15


    A.男生成绩的四分位距大于女生成绩的四分位距
    B.男生成绩的四分位距小于女生成绩的四分位距
    C.男生成绩的平均数大于女生成绩的平均数
    D.男生成绩的平均数小于女生成绩的平均数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（ ）
    A.
    B.
    C.
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=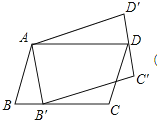

    查看答案和解析>>

    同步练习册答案