
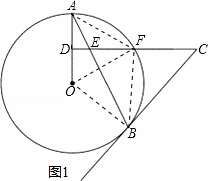
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.(4分+4分+4分)
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
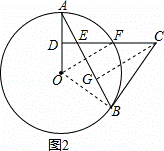
(3)如果CD=15,BE=10, ,求⊙O的半径.
,求⊙O的半径.

解答: (1)证明:连接OB∵OB=OA,CE=CB,∴∠A=∠OBA,∠CEB=∠ABC
又∵CD⊥OA ∴∠A+∠AED=∠A+∠CEB=90°∴∠OBA+∠ABC=90°
∴OB⊥BC ∴BC是⊙O的切线.
(2)解:如图1,连接OF,AF,BF,∵DA=DO,CD⊥OA,
∴AF=OF,∵OA=OF,∴△OAF是等边三角形,∴∠AOF=60°∴∠ABF=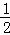 ∠AOF=30°;
∠AOF=30°;
(3)解:如图2,过点C作CG⊥BE于G,∵CE=CB,∴EG=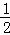 BE=5,
BE=5,
∵∠ADE=∠CGE=90°,∠AED=∠GEC,∴∠GCE=∠A,∴△ADE∽△CGE,
在RtECG中,∵CG=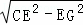 =12,∵CD=15,CE=13,∴DE=2,
=12,∵CD=15,CE=13,∴DE=2,
∵△ADE∽△CGE,∴ ,∴AD=
,∴AD=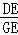 ,CG=
,CG=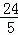 ,∴⊙O的半径OA=2AD=
,∴⊙O的半径OA=2AD= .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图6所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )
A.12 B.16 C.20 D.24
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6 ,DE=3.
,DE=3.
求:(1) ⊙O的半径;(2)弦AC的长;(3)阴影部分的面积.
(3分+3分+4分)
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,在数轴上点A所表示的数x的范围是( )
A.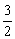 sin30°<x<sin60°;B.cos30°<x<
sin30°<x<sin60°;B.cos30°<x< 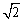 cos45°;
cos45°;
C.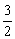 tan30°<x<tan45°;D.3cos60°<x<
tan30°<x<tan45°;D.3cos60°<x<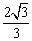 tan60°。
tan60°。
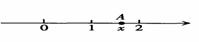
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=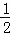 x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣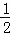 x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下:
(1)P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒 个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?
个单位的速度运动到A后停止,当点E的坐标是多少时,点M在整个运动中用时最少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com