
| A. | 最小的有理数是0 | |
| B. | 射线OM的长度是5cm | |
| C. | 两数相加,和一定大于任何一个加数 | |
| D. | 两点确定一条直线 |
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:填空题
 如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.
如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
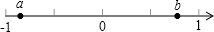 有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.
有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
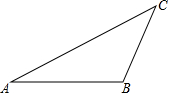 如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):
如图,已知:△ABC,请按下列要求用尺规作图(保留痕迹,不写作法及证明):查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x=-\frac{1}{3}$ | B. | x=-1 | C. | x=-11 | D. | $x=\frac{11}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com